题目内容
以下四个命题
（1）在△ABC中，内角A，B，C的对边分别为a，b，c，且bsinA=acosB，则B=
（2）设
，
是两个非零向量且|
•
=|
||
|，则存在实数λ，使得
=λ
；
（3）方程sinx-x=0在实数范围内的解有且仅有一个；
（4）a，b∈R且a3-3b＞b3-3a则a＞b；
其中正确的个数有（ ）
（1）在△ABC中，内角A，B，C的对边分别为a，b，c，且bsinA=acosB，则B=
| π |
| 4 |
（2）设
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
（3）方程sinx-x=0在实数范围内的解有且仅有一个；
（4）a，b∈R且a3-3b＞b3-3a则a＞b；
其中正确的个数有（ ）
| A．1个 | B．2个 | C．3 | D．4个 |
①由正弦定理知，
=
，即bsinA=asinB，
又由bsinA=acosB知，∴sinB=cosB，则B=
，故①正确；
②由于|
•
|=|
||
|，则cosθ=±1，
所以两向量
，
共线，则存在实数λ，使得
=λ
，故②正确；
③令f（x）=sinx-x，则f′（x）=1-cosx≥0恒成立，
所以x-sinx=0至多有一个解，
因为x=0 时，x-sinx=0，所以只有这一个解，故③正确；
④由于a3-3b＞b3-3a，则a3-b3+3a-3b＞0，
整理得（a-b）（a2+ab+b2+3）＞0，即(a-b)[(a+
b)2+
b2+3)＞0，所以a＞b，
由于a＞b，则a2+3＞b2+3，故a（a2+3）＞b（b2+3），整理得a3-3b＞b3-3a，故④正确．
| a |
| sinA |
| b |
| sinB |
又由bsinA=acosB知，∴sinB=cosB，则B=
| π |
| 4 |
②由于|
| a |
| b |
| a |
| b |
所以两向量
| a |
| b |
| b |
| a |
③令f（x）=sinx-x，则f′（x）=1-cosx≥0恒成立，
所以x-sinx=0至多有一个解，
因为x=0 时，x-sinx=0，所以只有这一个解，故③正确；
④由于a3-3b＞b3-3a，则a3-b3+3a-3b＞0，
整理得（a-b）（a2+ab+b2+3）＞0，即(a-b)[(a+
| 1 |
| 2 |
| 3 |
| 4 |
由于a＞b，则a2+3＞b2+3，故a（a2+3）＞b（b2+3），整理得a3-3b＞b3-3a，故④正确．
练习册系列答案
全能闯关100分系列答案
相关题目
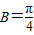
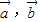是两个非零向量且|
=|
||
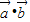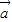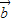|，则存在实数λ，使得
；
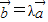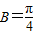
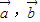是两个非零向量且|
=|
||
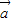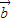|，则存在实数λ，使得
；
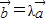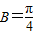
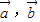是两个非零向量且|
=|
||
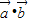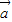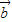|，则存在实数λ，使得
；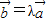