题目内容
如图3-3-25,在长为4宽为2的矩形中有一以矩形的长为直径的半圆,试用随机模拟法近似计算半圆面积,并估计π值.
图3-3-25
解析:设事件A：“随机向矩形内投点,所投的点落在半圆内”.
(1)利用计算机或计算机产生两组0到1区间的均匀随机数,x1=rand,y1=rand.
(2)经过伸缩平移变换,x=x1*4-2,y=y1*2.
(3)统计出试验总数N和满足条件x2+y2＜4的点(x,y)的个数N1.
(4)计算频率fn(A)=
,即为概率P(A)的近似值.
半圆的面积为S1=2π,矩形的面积为S=8.由几何概型概率公式得
P(A)=
,所以
=
.所以
即为π的近似值.
练习册系列答案
名校课堂系列答案
相关题目
某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．现从符合条件的志愿者中随机抽取100名按年龄分组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示．
（2012•朝阳区一模）某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．
的值为多少时,能使D1M⊥平面EFB1？并给出证明.
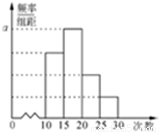
对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，恨据此数据作出了如图所示的频数与频率的统计表和频率分布直方图：
（I）求出表中M、p及图中a的值；
（II）学校诀定对参加社区服务的学生进行表彰，对参加活动次数在[25，30）区间的每个学生发放价值80元的学习用品，对参加活动次数在[20，25）区间的每个学生发放价值60元的学习用品，对参加活动次数在[15，20）区间的每个学生发放价值40元的学习用品，对参加活动次数在[10，15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，求此二人所获得学习用品价值之差的绝对值不超过20元的概率．
| 分组 | 频数 | 频率 |
| [10，15） | 6 | 0.3 |
| [15，20） | 8 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.1 |
| 合计 | M | 1 |
（II）学校诀定对参加社区服务的学生进行表彰，对参加活动次数在[25，30）区间的每个学生发放价值80元的学习用品，对参加活动次数在[20，25）区间的每个学生发放价值60元的学习用品，对参加活动次数在[15，20）区间的每个学生发放价值40元的学习用品，对参加活动次数在[10，15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，求此二人所获得学习用品价值之差的绝对值不超过20元的概率．