题目内容
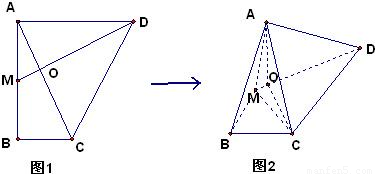
如图1,ABCD为直角梯形,AD∥BC,∠DAB=| π |
| 2 |
| 5 |
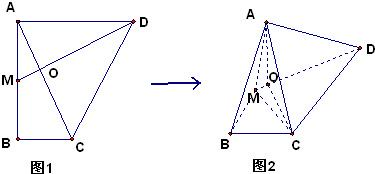
(Ⅰ)求证:平面MDA⊥平面OAC;
(Ⅱ)求直线AD与平面AMC所成角的余弦值.
分析:(I)欲证平面AOC⊥平面MDA,根据面面垂直的判定定理可知在平面MDA内一直线与平面AOC垂直,而根据题意可得MD⊥平面AOC;
(Ⅱ)建系以OC为x轴,以OD为y轴,以OA为z轴建立空间直角坐标系,求出平面AMC的法向量,以及直线AD所在向量,然后根据两向量的夹角公式求出所成角的正弦的,即可求出直线AD与平面AMC所成角的余弦值.
(Ⅱ)建系以OC为x轴,以OD为y轴,以OA为z轴建立空间直角坐标系,求出平面AMC的法向量,以及直线AD所在向量,然后根据两向量的夹角公式求出所成角的正弦的,即可求出直线AD与平面AMC所成角的余弦值.
解答:解:(Ⅰ)∵AB=AD,AM=BC,∠BAC=∠MAD,∴△AMD≌△ABC,∴∠BAC=∠ADM,
又∵∠BAC+∠CAD=90°,∴∠ADM+∠CAD=90°,∴AC⊥MD,∴AO⊥MD,OC⊥MD,
∴MD⊥平面AOC,∴平面AOC⊥平面MDA.
(Ⅱ)如图建系,

则C(3,0,0),A(0,0,2),D(0,4,0),M(0,-1,0),
∴
=(0,1,2),
=(3,1,0),设
⊥平面AMC,
=(x,y,z),
则
,∴
=(
,-2,1),
∵
=(0,4,-2),∴sinθ=
,,则cosθ=
.
∴直线AD与平面AMC所成角的余弦值为
.
又∵∠BAC+∠CAD=90°,∴∠ADM+∠CAD=90°,∴AC⊥MD,∴AO⊥MD,OC⊥MD,
∴MD⊥平面AOC,∴平面AOC⊥平面MDA.
(Ⅱ)如图建系,

则C(3,0,0),A(0,0,2),D(0,4,0),M(0,-1,0),
∴
| MA |
| MC |
| n |
| n |
则
|
| n |
| 2 |
| 3 |
∵
| AD |
3
| ||
| 7 |
| 2 |
| 7 |
∴直线AD与平面AMC所成角的余弦值为
| 2 |
| 7 |
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定及线面所成角的计算,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 如图,矩形ABCD的对角线AC,BD交于O,AB=4,AD=3.沿AC把△ACD折起,使二面角D1-AC-B为直二面角.
如图,矩形ABCD的对角线AC,BD交于O,AB=4,AD=3.沿AC把△ACD折起,使二面角D1-AC-B为直二面角.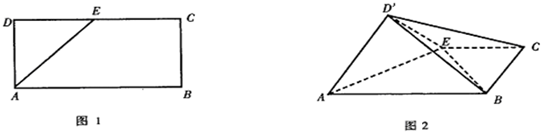
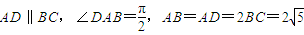 ,M是AB的中点,AC与MD交于O点,把△AMD沿着MD折起,使得二面角A-MD-C为直二面角形成图2.
,M是AB的中点,AC与MD交于O点,把△AMD沿着MD折起,使得二面角A-MD-C为直二面角形成图2.