题目内容
已知偶函数f(x),当x>0时,f(x)= +lnx(e=2.7182…为自然对数的底),则函数f(x)的零点不可能在区间内.
+lnx(e=2.7182…为自然对数的底),则函数f(x)的零点不可能在区间内.
- A.(-1,0)
- B.(0,1)
- C.(-
 ,
, )
) - D.(
 ,1)
,1)
C
分析:x>0时,f(x)为增函数,又f(x)为偶函数,先考察x>0时,f(x)的零点情况,再根据偶函数的图象关于y轴对称,可得函数f(x)的零点的整体情况.
解答:x>0时,f(x)为增函数,又f(x)为偶函数,先考察x>0时,f(x)的零点情况.
f(1)=1>0,f( )=
)=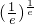 -1=
-1= -1<0,
-1<0,
由f(1)f( )<0知,x>0时,时f(x)的零点在区间(
)<0知,x>0时,时f(x)的零点在区间( ,1)内,又f(x)为偶函数,
,1)内,又f(x)为偶函数,
所以另一零点在区间(-1,- )内,
)内,
故选 C.
点评:本题主要考查了函数的零点存在定理,函数的奇偶性和单调性、概念,属于基础题.
分析:x>0时,f(x)为增函数,又f(x)为偶函数,先考察x>0时,f(x)的零点情况,再根据偶函数的图象关于y轴对称,可得函数f(x)的零点的整体情况.
解答:x>0时,f(x)为增函数,又f(x)为偶函数,先考察x>0时,f(x)的零点情况.
f(1)=1>0,f(
 )=
)=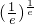 -1=
-1= -1<0,
-1<0,由f(1)f(
 )<0知,x>0时,时f(x)的零点在区间(
)<0知,x>0时,时f(x)的零点在区间( ,1)内,又f(x)为偶函数,
,1)内,又f(x)为偶函数,所以另一零点在区间(-1,-
 )内,
)内,故选 C.
点评:本题主要考查了函数的零点存在定理,函数的奇偶性和单调性、概念,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目