题目内容
16．已知a、b、c分别为△ABC三个内角A、B、C的对边，a=$\sqrt{3}$bsinA-acosB，则角B=60°．分析 利用正弦定理把已知的等式化边为角，由两角和与差的正弦函数公式化简，结合特殊角的三角函数值即可求得B的值．
解答 解：由a=$\sqrt{3}$bsinA-acosB，
由正弦定理得：$\sqrt{3}$sinBsinA-sinAcosB-sinA=0，
∵sinA≠0，
∴$\sqrt{3}$sinB-cosB=1．
即sin（B-30°）=$\frac{1}{2}$．
∵0°＜B＜180°，
∴-30°＜B-30°＜150°，
∴B-30°=30°，
故答案为：60°．
点评 本题考查了解三角形，训练了正弦定理的应用，考查了三角函数的两角和与差的正弦函数公式，属于基本知识的考查．
练习册系列答案
口算能手系列答案
相关题目
6．在平面直角坐标系中，O为坐标原点，A（1，0），B（0，-$\sqrt{3}$），点D是圆C：（x+1）2+y2=1上的动点，则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最大值为（ ）
| A． | 2 | B． | $\sqrt{3}$+1 | C． | $\sqrt{3}$+$\sqrt{2}$ | D． | $\sqrt{3}$+2 |
7．“a=1”是“直线l：y=kx+a与圆C：x2-2x+y2=0相交”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
4．在△ABC中，A=60°，若a，b，c成等比数列，则$\frac{bsinB}{c}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
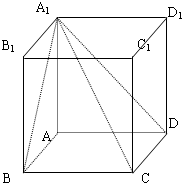如图，长方体ABCD-A1B1C1D1的AA1=1，底面ABCD的周长为4．