题目内容
已知平面区域D:
,?(a,b)∈D,a-2b≥0的概率是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:分别计算事件A的区域面积及平面区域 D的面积,代入几何概率的计算公式P(A)=
进行计算可求
| 构成事件A的区域面积 |
| 试验的全部结果所构成的区域面积 |
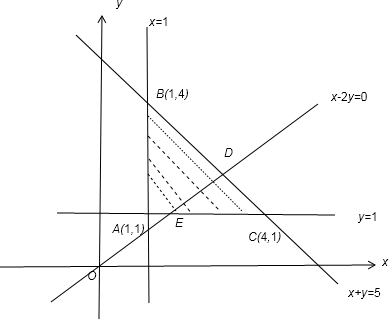
解答:解:由线性规划的知识可得,平面区域D即为图中的△ABC的区域,
且A(1,1) B(1,4) C(4,1)
∴SABC=
×3×3=
而a-2b≥0的平面区域即为图中的△DCE区域,D(
,
) E(2,1)
∴SEDC=
×
×2=
∴P=
=
=
且A(1,1) B(1,4) C(4,1)
∴SABC=
| 1 |
| 2 |
| 9 |
| 2 |
而a-2b≥0的平面区域即为图中的△DCE区域,D(
| 10 |
| 3 |
| 5 |
| 3 |
∴SEDC=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
∴P=
| S△EDC |
| SABC |
| ||
|
| 4 |
| 27 |

点评:本题考查了几何概率与面积有关的模型:计算公式P(A)=
,常见的类型有:①与长度有关的几何概率②与面积有关的几何概率③与体积有关的几何概率
| 构成事件A的区域面积 |
| 试验的全部结果所构成的区域面积 |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
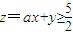 为事件A,则使
为事件A,则使 的常数a有( )
的常数a有( )