题目内容
【题目】△ABC的内角A，B，C所对的边分别为a，b，c， 
=（ 
，1）， 
=（sinA，cosA）， 与 的夹角为60°． （Ⅰ）求角A的大小；
（Ⅱ）若sin（B﹣C）=2cosBsinC，求 
的值．
【答案】解：（Ⅰ）∵ 
=（ 
，1）， 
=（sinA，cosA）， 与 的夹角为60°， ∴ = sinA+cosA=| || |cos60°，
即2sin（A+ 
）=2×1× 
=1，
即sin（A+ ）= ，
则A+ = 或 
，
则A=0（舍）或A= 
；
（Ⅱ）若sin（B﹣C）=2cosBsinC，
则sinBcosC﹣cosBsinC=2cosBsinC，
即sinBcosC=3cosBsinC，
即tanB=3tanC，
即tan（ 
﹣C）=3tanC，
即 
=3tanC， ﹣tanC=3tanC+3 tan2C，
即3 tan2C+4tanC﹣ =0，
则tanC=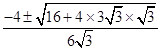 
= 
，
∵B+C= ，∴0＜C＜
则tanC＞0，∴tanC= 
，
由sinBcosC=3cosBsinC，
得 
= 
= 
= 
= 
+ 
，
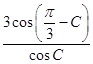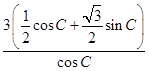即 
= 
+ = + 
× = 
【解析】（Ⅰ）根据向量夹角公式以及向量数量积的坐标公式和定义建立方程关系进行求解解求角A的大小；（Ⅱ）若sin（B﹣C）=2cosBsinC，利用正弦定理以及两角和差的余弦公式进行化简整理即可求 
的值．
【考点精析】认真审题，首先需要了解余弦定理的定义(余弦定理:
;
;
)．
练习册系列答案
相关题目
