题目内容
已知函数f(x)=2ax3-3ax2+1,g(x)=-| a |
| 4 |
| 3 |
| 2 |
(I)当a=1时,求函数y=f(x)的单调区间;
(II)若任意给定的x0∈[0,2],在[0,2]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
分析:(I)由题意先把a代入使得函数f(x)具体,再利用导函数求其单调区间;
(II)由题意可以把问题转化为求函数f(x)和函数g(x)的值域,并有题意转化为两个函数的值域的关系问题.
(II)由题意可以把问题转化为求函数f(x)和函数g(x)的值域,并有题意转化为两个函数的值域的关系问题.
解答:解:(I)f'(x)=6x2-6x=6x(x-1).
由f'(x)>0,得x>1或x<0;
由f'(x)<0,得0<x<1;
故函数f(x)的单调递增区间是(-∞,0],[1,+∞);
单调递减区间是[0,1].
(II)f′(x)=6ax2-6ax=6ax(x-1).
①当a=0时,显然不可能;
②当a>0时,函数f(x)的变化情况如下表所示
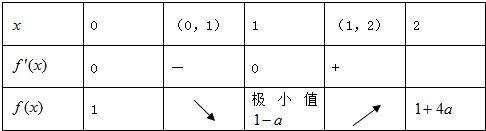
又因为当a>0时,g(x)=-
x+
在[0,2]上是减函数,
对任意x∈[0,2],g(x)∈[-
+
,
],不合题意;
③当a<0时,函数f(x)的变化情况如下表所示
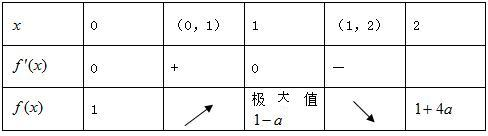
又因为当a<0时,g(x)=-
x+
在[0,2]上是增函数,
对任意x∈[0,2],g(x)∈[
,-
+
],
由题意可得,-
+
<1-a
∴a<-1
综上,a的取值范围为(-∞,-1).
由f'(x)>0,得x>1或x<0;
由f'(x)<0,得0<x<1;
故函数f(x)的单调递增区间是(-∞,0],[1,+∞);
单调递减区间是[0,1].
(II)f′(x)=6ax2-6ax=6ax(x-1).
①当a=0时,显然不可能;
②当a>0时,函数f(x)的变化情况如下表所示

又因为当a>0时,g(x)=-
| a |
| 4 |
| 3 |
| 2 |
对任意x∈[0,2],g(x)∈[-
| a |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
③当a<0时,函数f(x)的变化情况如下表所示

又因为当a<0时,g(x)=-
| a |
| 4 |
| 3 |
| 2 |
对任意x∈[0,2],g(x)∈[
| 3 |
| 2 |
| a |
| 2 |
| 3 |
| 2 |
由题意可得,-
| a |
| 2 |
| 3 |
| 2 |
∴a<-1
综上,a的取值范围为(-∞,-1).
点评:(I)在此重点考查了利用函数的导函数求其单调区间并且还考查了一元二次方程的求解方法;
(II)在此主要考查了等价转化的思想,还有利用导函数求函数的最值并考查了含有字母时分类讨论的思想,及集合之间的关系.
(II)在此主要考查了等价转化的思想,还有利用导函数求函数的最值并考查了含有字母时分类讨论的思想,及集合之间的关系.

练习册系列答案
相关题目