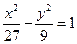题目内容
抛物线 的准线方程是( )
的准线方程是( )
A. | B.y=2 | C. | D.y=4 |
B
解析考点:抛物线的简单性质.
专题:计算题.
分析:先根据抛物线方程的标准形式,再根据抛物线的性质求出其准线方程即可.
解答:解:抛物线的方程为抛物线x2=-8y,故p=4,
其准线方程为y=2;
故选B
点评:本题考查抛物线的简单性质,解题关键是记准抛物线的标准方程,别误认为p=-4,因看错方程形式马虎导致错误.

练习册系列答案
相关题目
双曲线 的渐近线方程是
的渐近线方程是
A. | B. | C. | D. |
双曲线方程为 ,则它的右焦点坐标为( )
,则它的右焦点坐标为( )
A. | B. | C. | D. |
已知椭圆C: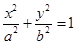
 的离心率为
的离心率为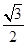 ,过右焦点
,过右焦点 且斜率为
且斜率为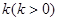 的直线与椭圆C相交于
的直线与椭圆C相交于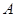 、
、 两点.若
两点.若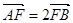 ,则
,则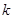 =( )
=( )
A. | B.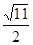 | C.2 | D. |
椭圆 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( )
| A.2 | B.3 | C.5 | D.7 |
如果椭圆 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A.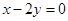 | B.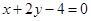 |
C. | D.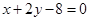 |
过点P(2,-2)且与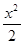 - y 2=1有相同渐近线的双曲线方程是 ( )
- y 2=1有相同渐近线的双曲线方程是 ( )
A. | B.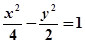 | C. | D.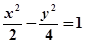 |
 和双曲线
和双曲线 有相同的焦点,则实数
有相同的焦点,则实数 的值是( )
的值是( ) B
B  C 5 D 9
C 5 D 9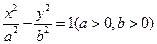 的一条渐近线方程是y=
的一条渐近线方程是y=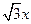 ,它的一个焦点在抛物线
,它的一个焦点在抛物线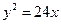 的准线上,则双曲线的方程为( )
的准线上,则双曲线的方程为( )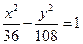 B
B 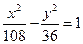
 C
C  D
D