题目内容
下列四个命题:
①在 中,若
中,若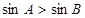 ,则
,则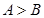 ;
;
②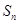 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,则
,则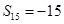 ;
;
③数列 的前n项和为
的前n项和为 且满足
且满足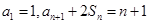 ,则
,则
④数列 满足
满足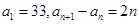 ,则
,则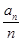 的最小值为
的最小值为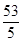
其中正确的命题序号 (注:把你认为正确的序号都填上)
①③
解析试题分析:由三角形的性质知,在 中,若
中,若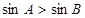 ,则
,则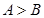 ,故命题①正确;对于命题②:∵
,故命题①正确;对于命题②:∵ ,∴
,∴ ,∴
,∴ ,错误;对于命题③:∵
,错误;对于命题③:∵ ,∴
,∴ ,两式相减得
,两式相减得 ,又
,又 ,所以数列
,所以数列 的奇数项为1,偶数项为0,所以
的奇数项为1,偶数项为0,所以 ,正确;对于命题④:∵
,正确;对于命题④:∵ ,∴
,∴ ,
, ,…,
,…, ,这(n-1)个式子相加得
,这(n-1)个式子相加得 ,∴
,∴ ,∴
,∴ ,根据对号函数的单调性知,当n=6时,
,根据对号函数的单调性知,当n=6时,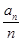 有最小值为
有最小值为 ,错误;综上正确的命题为①③
,错误;综上正确的命题为①③
考点:本题考查了三角形的性质及数列的性质及前N和的运用
点评:此类问题比较综合,掌握数列的通项公式及其求法、数列的性质等知识是解决此类问题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ”是“命题
”是“命题 ”成立的必要不充分条件,则实数
”成立的必要不充分条件,则实数 的取值范围为_________________.
的取值范围为_________________.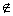 M”的逆否命题是:若b∈M,则a
M”的逆否命题是:若b∈M,则a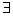 x0∈R,x
x0∈R,x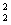 -x0-1>0”的否定
-x0-1>0”的否定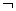 P:“
P:“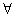 x∈R,x2-x-1≤0”.
x∈R,x2-x-1≤0”. 的渐近线方程为
的渐近线方程为 ;
; “
“ ,
, ”是真命题;
”是真命题; ,当变量
,当变量 增加
增加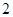 个单位,其预报值平均增加
个单位,其预报值平均增加 个单位;
个单位;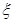 服从正态分布
服从正态分布 ,若
,若 ,则
,则 ;
; ,
, ,
, ,
, ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为 ,(
,( )
)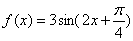 有以下命题:
有以下命题: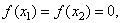 则
则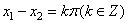 ; ②
; ②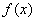 图象与
图象与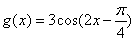 图 象相同;
图 象相同; 上是减函数; ④
上是减函数; ④ 对称。
对称。 x∈R,x2-x+3>0的否定是_______________________________。
x∈R,x2-x+3>0的否定是_______________________________。 ,
, ,
, 是
是 的充分条件,则实数
的充分条件,则实数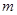 的取值范围是________
的取值范围是________  :
: ,
, .则命题
.则命题 是: 。
是: 。 则“
则“ ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件; 时,函数
时,函数 的最小值为2;
的最小值为2; ”与命题“
”与命题“ 或
或 ”都是真命题,则命题
”都是真命题,则命题 ,则
,则 .
.