题目内容
已知点A，B，C是不在同一直线上的三个点，O是平面ABC内一定点，P是△ABC内的一动点，若
-
=λ(
+
)，λ∈[0，+∞），则点P的轨迹一定过△ABC的（ ）
| OP |
| OA |
| AB |
| 1 |
| 2 |
| BC |
| A、外心 | B、内心 | C、重心 | D、垂心 |
分析：设出BC的中点D，利用向量的运算法则化简
+
；
-
据向量共线的充要条件得到P在三角形的中线上，利用三角形的重心定义：三中线的交点，得到选项
| AB |
| 1 |
| 2 |
| BC |
| OP |
| OA |
解答：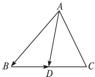
解：如图，取BC的中点D，连接AD，
则
+
=
+
=
．又
-
=λ(
+
)，
∴
-
=λ
，即
=λ
．
又λ∈[0，+∞），
∴P点在射线AD上．
故P的轨迹过△ABC的重心．
故选C
解：如图，取BC的中点D，连接AD，则
| AB |
| 1 |
| 2 |
| BC |
| AB |
| BD |
| AD |
| OP |
| OA |
| AB |
| 1 |
| 2 |
| BC |
∴
| OP |
| OA |
| AD |
| AP |
| AD |
又λ∈[0，+∞），
∴P点在射线AD上．
故P的轨迹过△ABC的重心．
故选C
点评：本题考查向量的运算法则、向量共线的充要条件、三角形的重心定义．
练习册系列答案
相关题目
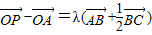，λ∈[0，+∞），则点P的轨迹一定过△ABC的（ ）
，λ∈[0，+∞），则点P的轨迹一定过△ABC的（ ）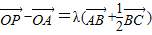
，λ∈[0，+∞），则点P的轨迹一定过△ABC的（ ）
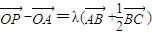，λ∈[0，+∞），则点P的轨迹一定过△ABC的（ ）