题目内容
5.集合M={x|x2≤2x},N={y|y=1-x,x∈M},则M∩N等于( )| A. | {x|-1≤x≤0} | B. | {x|1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
分析 先求出集合M,讲M中的x代入y=1-x,求出y的范围,确定出N,求出M与N的交集即可.
解答 解:集合M={x|x2≤2x}={x|0≤x≤2}=[0,2]
N={y|y=1-x,x∈M}={y|-1≤y≤1}=[-1,1],
∴M∩N=[0,1].
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
15.(1-2x)10的展开式中,各项系数的和是( )
| A. | 1 | B. | 210 | C. | -1 | D. | 1或-1 |
16.如果向量$\overrightarrow a=(1,\;2)$,$\overrightarrow b=(4,\;3)$,那么等于$\overrightarrow a-2\overrightarrow b$( )
| A. | (9,8) | B. | (-7,-4) | C. | (7,4) | D. | (-9,-8) |
10.某商品销量q与售价p满足q=10-λp,总成本c与销量满足c=4+μq,销售收入r与售价及销量之间满足r=pq,其中λ,μ均为正常数,设利润=销售收入-总成本,则利润最大时的售价为( )
| A. | $\frac{10-λμ}{λ}$ | B. | $\frac{10+λμ}{λ}$ | C. | $\frac{10-λμ}{2λ}$ | D. | $\frac{10+λμ}{2λ}$ |
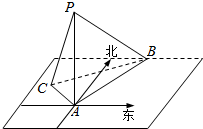 如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.
如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.