题目内容
设Mn={(十进制)n位纯小数0.
|ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则
=
.
. |
| a1a2…an |
| lim |
| n→∞ |
| Sn |
| Tn |
| 1 |
| 18 |
| 1 |
| 18 |
分析:根据ai只取0或1(i=1,2,…,n-1),可求Mn中元素的个数;在每一位(从第一位到第n-1位)小数上,数字0与1各出现2n-2次,第n位则1出现2n-1次,可求Sn,由此可得结论.
解答:解:由于ai只取0或1(i=1,2,…,n-1),Tn是Mn中元素的个数,所以Tn=2n-1;
在每一位(从第一位到第n-1位)小数上,数字0与1各出现2n-2次,第n位则1出现2n-1次
∴Sn=2n-2×0.11…1+2n-1×10-n,
∴
=
×
=
×
=
故答案为:
.
在每一位(从第一位到第n-1位)小数上,数字0与1各出现2n-2次,第n位则1出现2n-1次
∴Sn=2n-2×0.11…1+2n-1×10-n,
∴
| lim |
| n→∞ |
| Sn |
| Tn |
| 1 |
| 2 |
| 0.1 |
| 1-0.1 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 18 |
故答案为:
| 1 |
| 18 |
点评:本题考查数列的极限,考查等差数列的求和,考查学生的计算能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
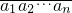 |ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则
|ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则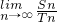 =________.
=________. |ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则
|ai只取0或1(i=1,2,…,n-1),an=1},Tn是Mn中元素的个数,Sn是Mn中所有元素的和,则 = .
= .