题目内容
设函数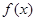 的定义域为
的定义域为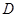 ,若存在非零常数
,若存在非零常数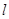 使得对于任意
使得对于任意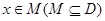 有
有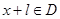 且
且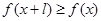 ,则称
,则称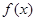 为
为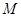 上的
上的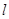 高调函数.对于定义域为
高调函数.对于定义域为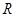 的奇函数
的奇函数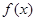 ,当
,当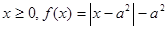 ,若
,若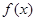 为
为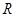 上的4高调函数,则实数
上的4高调函数,则实数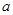 的取值范围为________.
的取值范围为________.
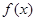 的定义域为
的定义域为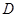 ,若存在非零常数
,若存在非零常数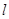 使得对于任意
使得对于任意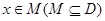 有
有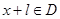 且
且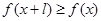 ,则称
,则称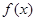 为
为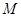 上的
上的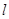 高调函数.对于定义域为
高调函数.对于定义域为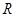 的奇函数
的奇函数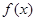 ,当
,当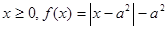 ,若
,若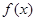 为
为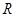 上的4高调函数,则实数
上的4高调函数,则实数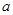 的取值范围为________.
的取值范围为________.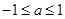
f(x)为R上的4高调函数, 则对任意X,有f(x+4)>=f(x)
f(x)=|x-
 |-
|-
x>
 =, f(x)=x-2
=, f(x)=x-2
0=<x<
 , f(x)=-x
, f(x)=-x由奇函数对称性,-
 2<x<0, f(x)=-x
2<x<0, f(x)=-xx
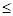 -
- , f(x)=x+
, f(x)=x+ 2
2因此f(x)在[-
 ,
, ]是减函数,其余区间是增函数。可作图形帮助理解。
]是减函数,其余区间是增函数。可作图形帮助理解。因此当X在[-2
 ,0]时f(x)>=0, 为保证f(x+4)>=f(x),x+4需跨过递减区间且f(x)>=0,即4>=4
,0]时f(x)>=0, 为保证f(x+4)>=f(x),x+4需跨过递减区间且f(x)>=0,即4>=4
所以有:

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
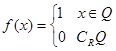 ,则
,则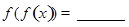 ;下面三个命题中,所有真命题的序号是 .
;下面三个命题中,所有真命题的序号是 . 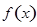 是偶函数;
是偶函数;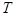 ,
,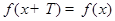 对
对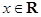 恒成立;
恒成立;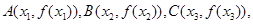 使得
使得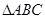 为等边三角形.
为等边三角形.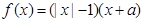 为奇函数,则
为奇函数,则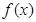 增区间为 .
增区间为 .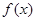 ,有下述命题:
,有下述命题: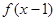 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称;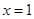 对称,则
对称,则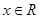 ,有
,有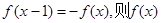 的周期为2;
的周期为2;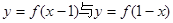 的图象关于直线
的图象关于直线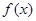 为定义在R上的奇函数,当
为定义在R上的奇函数,当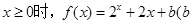 为常数),则
为常数),则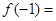 ( )
( )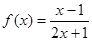 的对称中心是
的对称中心是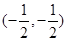 ;
; 的方程
的方程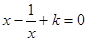 在
在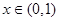 没有实数根,则
没有实数根,则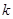 的取值范围是
的取值范围是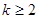 ;
;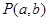 与点
与点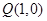 在直线
在直线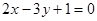 两侧,当
两侧,当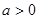 且
且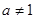 ,
,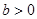 时,
时,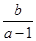 的取值范围为
的取值范围为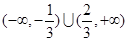 ;
;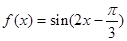 的图像向右平移
的图像向右平移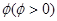 个单位后变为偶函数,则
个单位后变为偶函数,则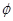 的最小值是
的最小值是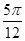 ; 其中正确的结论是:
; 其中正确的结论是: 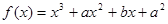 在
在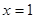 时有极值
时有极值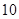 ,则
,则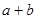 =_______.
=_______.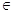 R,则下列各式成立的是
R,则下列各式成立的是 且
且 ,则
,则 ( )
( )

