Question

【题目】如图，分别过椭圆左、右焦点的动直线相交于点，与椭圆分别交于与不同四点，直线的斜率满足, 已知与轴重合时, .

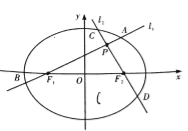
（1）求椭圆的方程；

（2）是否存在定点使得为定值，若存在，求出点坐标并求出此定值，若不存在，

说明理由.

Answer 1

【答案】（1）；（2）存在，，，.

【解析】

试题分析：（1）当与轴重合时，垂直于轴，得,得,从而得椭圆的方程；（2）由题目分析如果存两定点，则点的轨迹是椭圆或者双曲线 ，所以把坐标化，可得点的轨迹是椭圆，从而求得定点和点.

试题解析：当与轴重合时， , 即,所以垂直于轴，得，，, 得,椭圆的方程为.

焦点坐标分别为, 当直线或斜率不存在时，点坐标为或;

当直线斜率存在时，设斜率分别为, 设 由, 得：

, 所以: ，, 则：

. 同理：, 因为

, 所以, 即, 由题意知, 所以

， 设，则，即，由当直线或斜率不存在时，点坐标为或也满足此方程，所以点在椭圆上.存在点和点，使得为定值，定值为.