Question

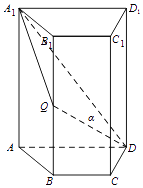
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
（1）求证：BD⊥平面ADG；
（2）求此多面体的全面积．

Answer 1

【答案】
（1）证明：在△BAD中，∵AB=2AD=2，∠BAD=60°，

∴由余弦定理可得BD= ，

则AB2=AD2+BD2，∴AD⊥BD．

在直平行六面体中，GD⊥平面ABCD，BD平面ABCD，

∴GD⊥BD，

又AD∩GD=D，∴BD⊥平面ADG；

（2）解：由已知可得，AG∥EF，AE∥GF，

∴四边形AEFG为平行四边形，

GD=AD=1，∴EF=AG= ．

EB=AB=2，∴GF=AE=2 ．

过G作GH∥DC交CF于H，得FH=2，∴FC=3．

过G作GM∥DB交BE于M，得GM=DB= ，ME=1，∴GE=2．

cos∠GAE= ，∴sin∠GAE= ．

．

该几何体的全面积S= ．

【解析】（1）在△BAD中，由余弦定理求得BD= ，可得AB2=AD2+BD2，得AD⊥BD．再由已知可得CD⊥BD，由线面垂直的判定可得BD⊥平面ADG；（2）由已知可得，AG∥EF，AE∥GF，得四边形AEFG为平行四边形，然后求出各面面积得答案．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．