题目内容
一直线过抛物线y2=2px(p>0)的焦点F,且交抛物线于A,B两点,C为抛物线准线的一点.(1)求证:∠ACB不可能是钝角;
(2)是否存在这样的点C,使得△ABC为正三角形?若存在,请求出点C的坐标;若不存在,请说明理由.
【答案】分析:(1)设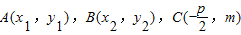 ,直线AB方程为
,直线AB方程为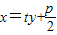 ,由
,由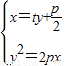 得:y2-2pty-p2=0,由此能够证明∠ACB不可能是钝角
得:y2-2pty-p2=0,由此能够证明∠ACB不可能是钝角
(2)假设存在点C,使得△ABC为正三角形.由(1)得:线段AB的中点为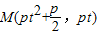 ,由此能够推导出存在点
,由此能够推导出存在点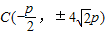 ,使得△ABC为正三角形.
,使得△ABC为正三角形.
解答:解:设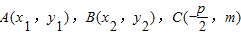 ,
,
直线AB方程为
由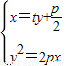 ,得:y2-2pty-p2=0,
,得:y2-2pty-p2=0,
则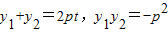
∴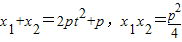 .
.
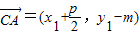 ,
,
∴
∴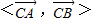 不可能为钝角,
不可能为钝角,
故∠ACB不可能是钝角
(2)假设存在点C,使得△ABC为正三角形
由(1)得:线段AB的中点为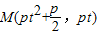
①若直线AB的斜率不存在,这时t=0,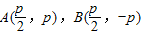 ,
,
点C的坐标只可能是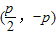 ,由
,由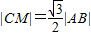 ,
,
得: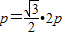 ,矛盾,于是直线AB的斜率必存在.
,矛盾,于是直线AB的斜率必存在.
②由CM⊥AB,得:kCM•kAB=-1,
即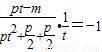 ,
,
∴m=pt3+2pt,
∴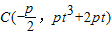
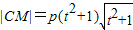 ,|AB|=2p(t2+1),
,|AB|=2p(t2+1),
由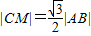 ,得:
,得: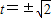 ,
,
∴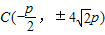
故存在点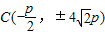 ,使得△ABC为正三角形.
,使得△ABC为正三角形.
点评:本题考查角不能为钝角的证明,判断是否存在满足条件的点使得三角形为正三角形.具体涉及到抛物线的简单性质,直线和抛物线的位置关系,是难题.
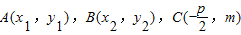 ,直线AB方程为
,直线AB方程为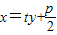 ,由
,由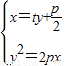 得:y2-2pty-p2=0,由此能够证明∠ACB不可能是钝角
得:y2-2pty-p2=0,由此能够证明∠ACB不可能是钝角(2)假设存在点C,使得△ABC为正三角形.由(1)得:线段AB的中点为
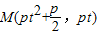 ,由此能够推导出存在点
,由此能够推导出存在点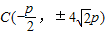 ,使得△ABC为正三角形.
,使得△ABC为正三角形.解答:解:设
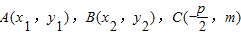 ,
,直线AB方程为

由
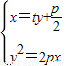 ,得:y2-2pty-p2=0,
,得:y2-2pty-p2=0,则
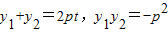
∴
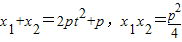 .
.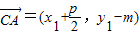 ,
,
∴

∴
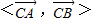 不可能为钝角,
不可能为钝角,故∠ACB不可能是钝角
(2)假设存在点C,使得△ABC为正三角形
由(1)得:线段AB的中点为
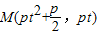
①若直线AB的斜率不存在,这时t=0,
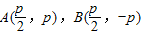 ,
,点C的坐标只可能是
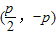 ,由
,由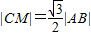 ,
,得:
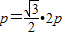 ,矛盾,于是直线AB的斜率必存在.
,矛盾,于是直线AB的斜率必存在.②由CM⊥AB,得:kCM•kAB=-1,
即
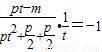 ,
,∴m=pt3+2pt,
∴
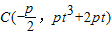
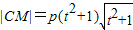 ,|AB|=2p(t2+1),
,|AB|=2p(t2+1),由
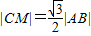 ,得:
,得: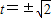 ,
,∴
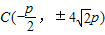
故存在点
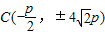 ,使得△ABC为正三角形.
,使得△ABC为正三角形.点评:本题考查角不能为钝角的证明,判断是否存在满足条件的点使得三角形为正三角形.具体涉及到抛物线的简单性质,直线和抛物线的位置关系,是难题.

练习册系列答案
相关题目