题目内容
已知非零向量 ,
, 的夹角为60°,且满足
的夹角为60°,且满足 ,,则
,,则
 的最大值为 .
的最大值为 .
【答案】分析:根据已知等式,平方得: -4
-4
 +4
+4 =4…(*),由向量
=4…(*),由向量 ,
, 的夹角为60°,得
的夹角为60°,得
 =
=

 ,代入(*)并化简整理,得4+2
,代入(*)并化简整理,得4+2
 =
= +4
+4 ,再利用基本不等式得到
,再利用基本不等式得到
 ≤2,得到当且仅当
≤2,得到当且仅当 =2
=2 时,
时,
 的最大值为1.
的最大值为1.
解答:解:∵
∴ =4,即
=4,即 -4
-4
 +4
+4 =4…(*)
=4…(*)
∵向量 ,
, 的夹角为60°,
的夹角为60°,
∴
 =
=
 cos60°=
cos60°=


代入(*),得 -2
-2
 +4
+4 =4,所以4+2
=4,所以4+2
 =
= +4
+4 ≥4
≥4

解之得:
 ≤2,当且仅当
≤2,当且仅当 =2
=2 时,等号成立
时,等号成立
∴
 =
=

 ,
,
 的最大值为1
的最大值为1
故答案为:1
点评:本题给出向量等式,在已知两个向量夹角为60度的情况下,求它们数量积的最大值,着重考查了平面向量数量积的公式和基本不等式求最值等知识,属于中档题.
 -4
-4
 +4
+4 =4…(*),由向量
=4…(*),由向量 ,
, 的夹角为60°,得
的夹角为60°,得
 =
=

 ,代入(*)并化简整理,得4+2
,代入(*)并化简整理,得4+2
 =
= +4
+4 ,再利用基本不等式得到
,再利用基本不等式得到
 ≤2,得到当且仅当
≤2,得到当且仅当 =2
=2 时,
时,
 的最大值为1.
的最大值为1.解答:解:∵

∴
 =4,即
=4,即 -4
-4
 +4
+4 =4…(*)
=4…(*)∵向量
 ,
, 的夹角为60°,
的夹角为60°,∴

 =
=
 cos60°=
cos60°=


代入(*),得
 -2
-2
 +4
+4 =4,所以4+2
=4,所以4+2
 =
= +4
+4 ≥4
≥4

解之得:

 ≤2,当且仅当
≤2,当且仅当 =2
=2 时,等号成立
时,等号成立∴

 =
=

 ,
,
 的最大值为1
的最大值为1故答案为:1
点评:本题给出向量等式,在已知两个向量夹角为60度的情况下,求它们数量积的最大值,着重考查了平面向量数量积的公式和基本不等式求最值等知识,属于中档题.

练习册系列答案
相关题目
 ,
, 的夹角为60°,且满足
的夹角为60°,且满足 ,,则
,,则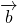 的最大值为________.
的最大值为________. ,
, 的夹角为60°,且满足
的夹角为60°,且满足 ,,则
,,则
 的最大值为 .
的最大值为 .












