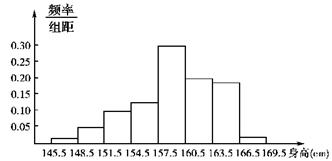
题目内容
(本小题满分12分)某汽车厂生产A、B两类轿车,每类轿车均有舒适型和标准型两种,某月的产量如下表:
按分层抽样的方法在该月生产的轿车中抽取50辆,其中A类轿车20辆。
(I)求x的值;
(II)用分层抽样的方法在B类轿车中抽取一个容量为6的样本,从样本中任意取2辆,求至少有一辆舒适轿车的概率。
(1)由 ,解得
,解得 ————4分
————4分
(2)法一:列举法
抽取容量为6的样本,则其中舒适型轿车为2辆,标准型轿车为4辆,可设舒适型轿车为 ,标准型轿车为
,标准型轿车为 ,
,
则从6辆的样本中任抽2辆的可能有 ,
, ,
, ,
, ,
, ,
, 共15种,
共15种,
至少有一辆是舒适型轿车的可能有 ,
, ,
, 共9种,
共9种,
所以至少有一辆是舒适型轿车的概率是 ----------------------12分
----------------------12分
法二:抽取容量为6的样本,则其中舒适性2辆;标准型4辆。 ————6分
法一: ————12分
————12分
解析

 阅读快车系列答案
阅读快车系列答案(12分)某市中学生田径运动会总分获得冠、亚、季军的代表队人数如下表,大会组委会为使颁奖仪式有序进行,用分层抽样的方法从三个代表队中抽取16人在前排就座,其中亚军队有5人. (1)求季军队中男运动员的人数(2)从前排就座的亚军队5人(3男2女)中随机抽取2人上台领奖请列出所有的基本事件,并求亚军队中有女生上台领奖的概率;
(1)求季军队中男运动员的人数(2)从前排就座的亚军队5人(3男2女)中随机抽取2人上台领奖请列出所有的基本事件,并求亚军队中有女生上台领奖的概率;
| 性别 名次 | 冠军 | 亚军 | 季军 |
| 男生 | 30 | 30 |  |
| 女生 | 30 | 20 | 30 |
(本题满分12分)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得
他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
| | A | B | C | D | E |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) | | | | | |
(2)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合计 | 正 正 | | | |
(12分)假设关于某市房屋面积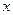 (平方米)与购房费用
(平方米)与购房费用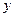 (万元),有如下的统计数据:
(万元),有如下的统计数据:
| x(平方米) | 80 | 90 | 100 | 110 |
| y(万元) | 42 | 46 | 53 | 59 |
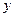 对
对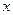 呈线性相关。
呈线性相关。(1)求回归直线方程;
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
公式:
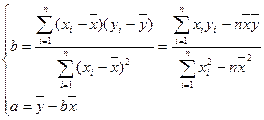
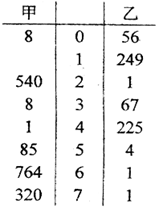
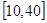 间的频率是多少?
间的频率是多少?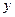 和
和 房屋的面积
房屋的面积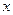 的数据:
的数据: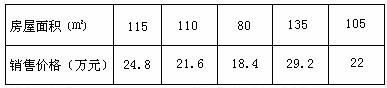
 归方程。(保留四位小数)
归方程。(保留四位小数)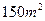 时的销售价格。
时的销售价格。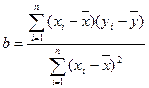 ,
,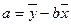
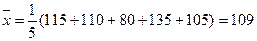 ,
,
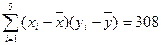 ,
,