题目内容
经过抛物线y2=4x的焦点作直线交该抛物线于A（x1，y1）、B（x2，y2）两点，如果|AB|=8，那么x1+x2=
- A.4
- B.6
- C.8
- D.10
B
分析：根据抛物线方程可求得准线方程，进而根据抛物线的定义可知|AB|=x1+2+x2+2答案可得．
解答：依题意可知p=2，
准线方程为x=-1，
根据抛物线的定义，
可知|AB|=x1+1+x2+1=8
∴x1+x2=6
故选B
点评：本题主要考查抛物线的应用，要牢记抛物线的定义，属基础题．
分析：根据抛物线方程可求得准线方程，进而根据抛物线的定义可知|AB|=x1+2+x2+2答案可得．
解答：依题意可知p=2，
准线方程为x=-1，
根据抛物线的定义，
可知|AB|=x1+1+x2+1=8
∴x1+x2=6
故选B
点评：本题主要考查抛物线的应用，要牢记抛物线的定义，属基础题．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
经过抛物线y2=4x的焦点，且方向向量为
=（1，2）的直线l的方程是（ ）
| a |
| A、x-2y-1=0 |
| B、2x+y-2=0 |
| C、x+2y-1=0 |
| D、2x-y-2=0 |
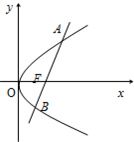已知直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A、B两点．