题目内容
若函数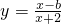 在(a,b+4)(b<-2)上的值域为(2,+∞),则ab=________.
在(a,b+4)(b<-2)上的值域为(2,+∞),则ab=________.

分析:本题考查的是函数的最值应用问题.在解答时可以先将函数变形为
 ,然后利用b的范围获得函数的单调性,又由于在(a,b+4)(b<-2)上的值域为(2,+∞),所以结合边界值的特点即可获得a、b的值,从而问题即可获得解答.
,然后利用b的范围获得函数的单调性,又由于在(a,b+4)(b<-2)上的值域为(2,+∞),所以结合边界值的特点即可获得a、b的值,从而问题即可获得解答.解答:将已知函数变形为
 ,
,又∵b<-2,∴b+2<0.
∴函数
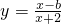 在(a,b+4)(b<-2)上为减函数,
在(a,b+4)(b<-2)上为减函数,∴

又∵值域为(2,+∞),
∴
 ,
, 趋向于+∞.
趋向于+∞.∴b=-4,a=-2,
∴ab=
 .
.故答案为:
 .
.点评:本题考查的是函数的最值应用问题.在解答的过程当中当中充分体现了函数的变形技巧、单调性的分析以及问题转化的能力.值得同学们体会反思.

练习册系列答案
相关题目
 ,则ab=________.
,则ab=________.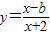 在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= .
在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= . 在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= .
在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= . 在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= .
在(a,b+4)(b<-2)上的值域为(2,+∞),则ab= .