题目内容
如果M（2，m），N（4，1），P（5，3+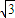
），Q（6，3）四个共圆，则m的值是（ ）A．1
B．3
C．5
D．7
【答案】分析：本题考查的知识点是圆的方程，由M（2，m），N（4，1），P（5，3+
），Q（6，3）四点共圆，我们可以根据N（4，1），P（5，3+
），Q（6，3）三点坐标，利用待定系数法求出圆的方程，然后将M（2，m）点由圆的方程，即可求出对应m的值．
解答：解：设圆的方程为x2+y2+Dx+Ey+F=0
∵点N（4，1），P（5，3+
），Q（6，3）都在圆上
故
解得
则圆的方程为x2+y2-8x-6y+21=0
将M（2，m）代入得：4+m2-16-6m+21=0
即：m2-6m+9=0
解得：m=3
故选B
点评：求圆的方程时，据条件选择合适的方程形式是关键．（1）当条件中给出的是圆上几点坐标，较适合用一般式，通过解三元一次方程组来得相应系数．（2）当条件中给出的圆心坐标或圆心在某直线上、圆的切线方程、圆的弦长等条件，适合用标准式．
），Q（6，3）四点共圆，我们可以根据N（4，1），P（5，3+），Q（6，3）三点坐标，利用待定系数法求出圆的方程，然后将M（2，m）点由圆的方程，即可求出对应m的值．解答：解：设圆的方程为x2+y2+Dx+Ey+F=0
∵点N（4，1），P（5，3+
），Q（6，3）都在圆上故
解得
则圆的方程为x2+y2-8x-6y+21=0
将M（2，m）代入得：4+m2-16-6m+21=0
即：m2-6m+9=0
解得：m=3
故选B
点评：求圆的方程时，据条件选择合适的方程形式是关键．（1）当条件中给出的是圆上几点坐标，较适合用一般式，通过解三元一次方程组来得相应系数．（2）当条件中给出的圆心坐标或圆心在某直线上、圆的切线方程、圆的弦长等条件，适合用标准式．
练习册系列答案
相关题目
如果M（2，m），N（4，1），P（5，3+
），Q（6，3）四个共圆，则m的值是（ ）
| 3 |
| A、1 | B、3 | C、5 | D、7 |
），Q（6，3）四个共圆，则m的值是