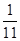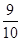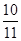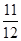题目内容
设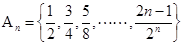
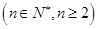 ,
,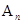 的所有非空子集中的最小元素的和为
的所有非空子集中的最小元素的和为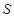 ,则
,则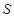 = .
= .
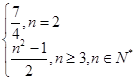
解析试题分析:这个问题主要是研究集合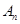 中的每个元素在和
中的每个元素在和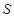 中分别出现多少次,事实上,以
中分别出现多少次,事实上,以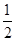 为例,集合
为例,集合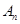 中比
中比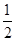 大的所有元素组成的集合
大的所有元素组成的集合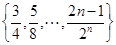 的所有子集共有
的所有子集共有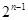 个,把
个,把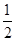 加进这些子集里形成新的集合,每个都是最小元素为
加进这些子集里形成新的集合,每个都是最小元素为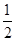 的集合
的集合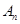 的子集,而最小元素为
的子集,而最小元素为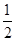 的集合
的集合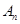 的子集也就是这些,故在
的子集也就是这些,故在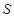 中
中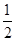 出现
出现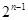 次,同理
次,同理 出现
出现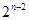 次,…,
次,…,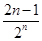 出现1次,所以有
出现1次,所以有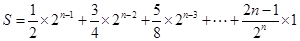
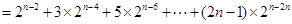 ,这个和用错位相减法可求得.
,这个和用错位相减法可求得.
考点:子集的个数,借位相减法求数列的和.

练习册系列答案
相关题目
各项均为正数的等比数列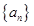 的前
的前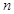 项和记为
项和记为 ( )
( )
| A.150 | B.-200 | C.150或-200 | D.-50或400 |
已知等差数列 的通项公式为
的通项公式为 ,设
,设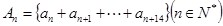 ,则当
,则当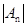 取得最小值是,n的值是 ( )
取得最小值是,n的值是 ( )
| A.17 | B.16 | C.15 | D.13 |
定义数列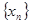 :
: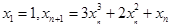 ;数列
;数列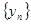 :
: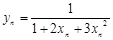 ;数列
;数列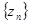 :
: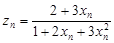 ;若
;若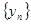 的前n项的积为
的前n项的积为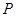 ,
,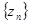 的前n项的和为
的前n项的和为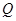 ,那么
,那么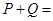 ( )
( )
A. | B.2 | C.3 | D.不确定 |
数列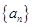 的通项公式
的通项公式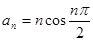 ,其前
,其前 项和为
项和为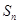 ,则
,则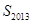 等于 ( )
等于 ( )
A.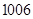 | B.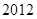 | C. | D. |
数列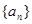 的前n项和为
的前n项和为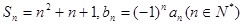 ,则数列
,则数列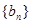 的前50项的和为( )
的前50项的和为( )
| A.49 | B.50 | C.99 | D.100 |
数列{an}的通项公式为an=(-1)n-1·(4n-3),则它的前100项之和S100等于( )
| A.200 | B.-200 | C.400 | D.-400 |
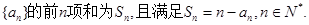
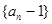 是等比数列;
是等比数列;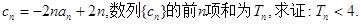
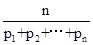 为
为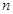 个正数
个正数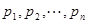 的“均倒数”.若已知数列
的“均倒数”.若已知数列 的前
的前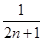 ,又
,又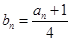 ,则
,则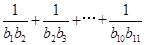 =( )
=( )