题目内容
数列{an}的通项公式为an=
，则这个数列的前30项中的最大项和最小项分别是（ ）
n-
| ||
n-
|
| A、a9，a10 |
| B、a10，a9 |
| C、a30，a10 |
| D、a9，a1 |
分析：把给出的数列的通项公式变形，把an看作n的函数，作出相应的图象，由图象分析得到答案．
解答：解：由an=
，
则an=
=1-
．
该函数在（0，
）和（
，+∞）上都是递增的，
图象如图，
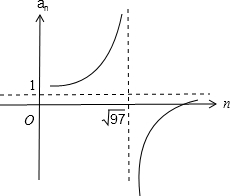
∵9＜
＜10．
∴这个数列的前30项中的最大项和最小项分别是a9，a10．
故选：A．
n-
| ||
n-
|
则an=
n-
| ||||||
n-
|
=1-
| ||||
n-
|
该函数在（0，
| 97 |
| 97 |
图象如图，
∵9＜
| 97 |
∴这个数列的前30项中的最大项和最小项分别是a9，a10．
故选：A．
点评：本题考查了数列的函数特性，考查了数形结合的解题思想，解答的关键是根据数列通项公式画出图象，是基础题．
练习册系列答案
相关题目
，Tn为数列{bn}的前n项和，求Tn．