Question

已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0），A（2，0）为长轴的一个端点，弦BC过椭圆的中心O，且

AC

•

BC

=0，|

OC

-

OB

|=2|

BC

-

BA

|，，则其焦距为（　　）

• A、

  2 6

  3

• B、

  4 3

  3

• C、

  4 6

  3

• D、

  2 3

  3

Answer 1

分析：由题意可知|

OC

|=|

OB

|=

1

2

|

BC

|，且a=2，进而可确定C（1，-1），代入椭圆方程，从而可求椭圆的焦距．

解答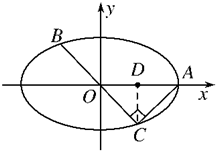：解：由题意可知|

OC

|=|

OB

|=

1

2

|

BC

|，且a=2，
又|

OC

-

OB

|=2|

BC

-

BA

|，
∴|

BC

|=2|

AC

|．
∴|

OC

|=|

AC

|．
又∵

AC

•

BC

=0，
∴

AC

⊥

BC

．
∴|

OC

|=|

AC

|=

2

．
如图，在Rt△AOC中，求得C（1，-1），代入椭圆方程得

1

4

+

(-1)2

b2

=1⇒b²=

4

3

，
∴c²=a²-b²=4-

4

3

=

8

3

．
∴c=

2 6

3

，2c=

4 6

3

，
故选C．

点评：本题重点考查椭圆的性质，考查向量知识的运用，解题的关键是求出点C的坐标，从而可求出椭圆的方程．