题目内容
函数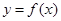 的图像如图所示,
的图像如图所示,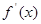 为
为 的导函数,则
的导函数,则 ,
,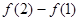 的大小关系是()
的大小关系是()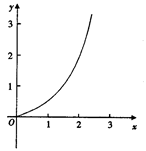
A.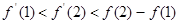 |
B.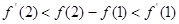 |
C.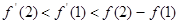 |
D.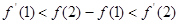 |
D
解析试题分析:函数图象的坡陡情况,对应着切线斜率的大小,而切线的斜率,是函数在切点的导函数值。所以,观察函数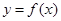 的图像可知,图象越来越陡,即切线的斜率越来越大,
的图像可知,图象越来越陡,即切线的斜率越来越大,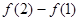 是(1,f(1))与(2,f(2))连线的斜率,所以,
是(1,f(1))与(2,f(2))连线的斜率,所以,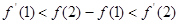 ,选D。
,选D。
考点:导数的几何意义,应用导数研究函数的单调性。
点评:简单题,函数图象的坡陡情况,对应着切线斜率的大小,而切线的斜率,是函数在切点的导函数值。

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
下列函数中,在区间 上为增函数的是( ).
上为增函数的是( ).
A.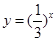 | B.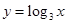 | C.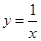 | D.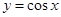 |
下列函数中,在其定义域内既是奇函数又是增函数的是
A.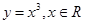 | B.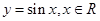 | C.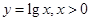 | D.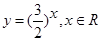 |
 是以
是以 为周期的奇函数,若
为周期的奇函数,若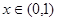 时,
时, ,则
,则 在区间
在区间 上是( )
上是( )
A.增函数且 | B.减函数且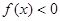 |
C.增函数且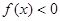 | D.减函数且 |
已知函数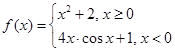 ,且方程
,且方程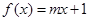 在区间
在区间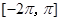 内有两个不等的实根,则实数
内有两个不等的实根,则实数 的取值范围( )
的取值范围( )
A.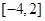 | B.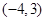 | C.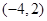 | D.[2,4] |
函数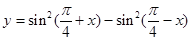 的值域是
的值域是
A.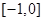 | B.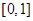 | C.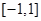 | D.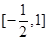 |
函数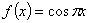 与函数
与函数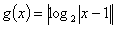 的图象所有交点的横坐标之和为
的图象所有交点的横坐标之和为
A.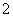 | B.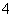 |
C.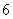 | D.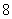 |
 的定义域为 ( )
的定义域为 ( )
 上的函数
上的函数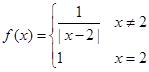 ,若关于
,若关于 的方程
的方程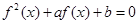 有3个不同实数解
有3个不同实数解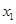 、
、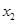 、
、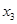 ,且
,且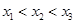 ,则下列说法中错误的是( )
,则下列说法中错误的是( )