题目内容
若tan(α+β)=![]() ,tan(β﹣
,tan(β﹣![]() )=
)=![]() ,则tan(α+
,则tan(α+![]() )= .
)= .
考点:
两角和与差的正切函数.
专题:
计算题.
分析:
把α+![]() 变为[(α+β)﹣(
变为[(α+β)﹣(![]() )],然后利用两角差的正切函数的公式化简所求的式子,整体代入即可求出值.
)],然后利用两角差的正切函数的公式化简所求的式子,整体代入即可求出值.
解答:
解:因为α+![]() =[(α+β)﹣(
=[(α+β)﹣(![]() )],且tan(α+β)=
)],且tan(α+β)=![]() ,tan(β﹣
,tan(β﹣![]() )=
)=![]() ,
,
则根据两角差的正切函数的公式得:
tan(α+![]() )=tan[(α+β)﹣(β﹣
)=tan[(α+β)﹣(β﹣![]() )]
)]
=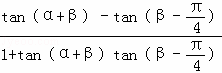 =
=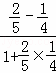 =
=![]()
故答案为![]()
点评:
考查学生会灵活变换角度来解决数学问题,利用两角和与差的正切函数的公式进行化简求值,以及利用整体代入的数学思想解决数学问题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若tanα+
=
,α∈(
,
),则sin(2α+
)的值为( )
| 1 |
| tanα |
| 10 |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|