题目内容
已知a，b∈R+，a+b=1
求证：
．
证明：∵a，b∈R+，a+b=1，∴
（当且仅当a=b=
时，等号成立）
∵
=ab+
+
=
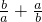-2，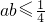
∴构造函数f（x）=
（x≤
）
∵x≤，∴
＜0
∴函数f（x）=在（0，]上单调递减
∴x=时，函数取得最小值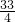
∴f（x）≥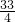
∴-2≥
∴
∴．
分析：先证明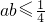，再证明-2≥，最后两边取对数，即可得到结论．
点评：本题考查不等式的证明，考查基本不等式的运用，考查函数的单调性，属于中档题．
（当且仅当a=b=
时，等号成立）∵
=ab+
+
=
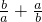-2，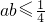
∴构造函数f（x）=
（x≤
）∵x≤
，∴
＜0∴函数f（x）=
在（0，]上单调递减∴x=
时，函数取得最小值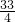
∴f（x）≥
∴
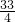
-2≥
∴
∴
．分析：先证明
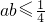，再证明-2≥，最后两边取对数，即可得到结论．点评：本题考查不等式的证明，考查基本不等式的运用，考查函数的单调性，属于中档题．
练习册系列答案
考前必练系列答案
相关题目
+
＞2.这四个式子中恒成立的是( )