题目内容
对于定义在![]() 上的函数
上的函数![]() ,若存
,若存![]() 在
在![]() ,对任意的
,对任意的![]() ,都有
,都有![]() 或者
或者![]() ,则称
,则称![]() 为函数
为函数![]() 在区间
在区间![]() 上的“下确界”或“
上的“下确界”或“![]() 上确界”.
上确界”.
(Ⅰ)求函数![]() 在
在![]() 上的“下确界”;
上的“下确界”;
(Ⅱ)若把“上确界”减去“下确界”的差称为函数![]() 在
在![]() 上的“极差
上的“极差![]() ”, 试
”, 试![]() 求函数
求函数![]() 在
在![]() 上的“极差
上的“极差![]() ”;
”;
(Ⅲ)类比函数![]() 的“极差
的“极差![]() ”的概念, 请求出
”的概念, 请求出![]() 在
在![]() 上的“极差
上的“极差![]() ”.
”.
解:(Ⅰ) 令![]() ,则
,则![]() ,
, ![]()
显然,![]() ,列表有:
,列表有:
| x | 0 | (0, x1) | x1 | (x1, 1) | 1 |
| | - | 0 | + | ||
| | | ↘ | 极小值 | ↗ | 1 |
所以,![]() 在
在![]() 上的“下确界”为
上的“下确界”为 ![]() . ………………4分
. ………………4分
(Ⅱ)①当![]() 时,
时,![]() ,
,![]() ,
,
极差![]()
![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,
,
极差![]()
![]() ;
;
③当![]() 时,
时, ![]() ,
,![]() ,极差
,极差![]()
![]() ;
;
④当![]() 时,
时,![]()
![]() ,
,
极差![]()
![]() ;
;
⑤当![]() 时,
时,![]() ,
,![]() ,极差
,极差![]()
![]() ;
;
⑥当![]() 时,
时, ![]() ,
, ![]() ,
,
极差![]()
![]() .
.
综上所述: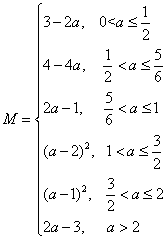
(Ⅲ) 因为![]() ,
,
当![]() 或
或![]() 时等号成立,所以
时等号成立,所以![]() 的最大值为1.
的最大值为1.
令![]() ,则
,则
![]()
令![]() ,则
,则
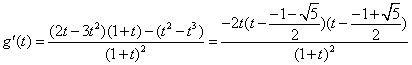 ,
,
令![]() ,得
,得![]() 是
是![]() 的极大值点,也是
的极大值点,也是![]() 的最大值点,
的最大值点,
![]() ,从而
,从而![]() ,
,
所以 ![]()
当![]() 时等号成立,所以
时等号成立,所以![]() 的最小值为
的最小值为![]() .
.
由此![]()

练习册系列答案
相关题目
 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 :
: ,若
,若  +
+
 ,
, 上的函数
上的函数 ,有如下四个命题:
,有如下四个命题: ,则函数
,则函数 则函数
则函数 则函数
则函数 恒过定点
恒过定点 .
. ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,求
,求 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 ,若
,若  +
+
 ,
, 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 ,若
,若  +
+
 ,
,