Question

如图,直三棱柱ABC—A₁B₁C₁中,AB=AC=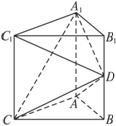AA₁=a,∠BAC=90°,D为棱B₁B的中点.

(1)证明A₁D⊥平面ADC;

(2)求异面直线A₁C与C₁D所成角的大小;

(3)求平面A₁CD与平面ABC所成二面角的大小(仅考虑锐角的情况).

Answer 1

(1)证明:∵△A₁B₁D和△ABD都为等腰直角三角形,

    ∴∠A₁DB₁=∠ADB=45°.∴∠A₁DA=90°,即A₁D⊥AD.

    又∵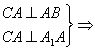CA⊥A₁D,

    ∴A₁D⊥平面ADC.

(2)解:连结AC₁交A₁C于E点,取AD中点F,连结EF、CF,则EF∥C₁D,

    ∴∠CEF是异面直线A₁C与C₁D所成的角(或补角).

    EF=C₁D=a,CE=A₁C=a,CF==a,在△CEF中,cos∠CEF==,∴∠CEF=arccos.

    则异面直线A₁C与C₁D所成角的大小为arccos.

(3)解:延长A₁D与AB的延长线交于G点,连结CG,

    过A作AH⊥CG于H点,连结A₁H,

    ∵A₁A⊥平面ABC,

    ∴A₁H⊥CG(三垂线定理).

    ∴∠A₁HA是二面角A₁CGA的平面角,即所求二面角的平面角.

    在Rt△ACG中,

    ∵AC=a,AG=2a,∴CG=a.

    ∴AH==a.

    在Rt△A₁AH中,tan∠A₁HA==,∴∠A₁HA=arctan,

    即所求的二面角的大小为arctan.