题目内容
设函数f(x)的导函数为f′(x),且f(x)=lnx+2x•f′(1),则f′(1)=
-1
-1
.分析:对函数f(x)的解析式求导,得到其导函数,把x=1代入导函数中,列出关于f'(1)的方程,进而得到f'(1)的值.
解答:解:求导得:f′(x)=
+2f′(1),
令x=1,得到f′(1)=2f′(1)+1,
解得:f′(1)=-1,
故答案为:-1
| 1 |
| x |
令x=1,得到f′(1)=2f′(1)+1,
解得:f′(1)=-1,
故答案为:-1
点评:本题主要考查了导数的运算,运用求导法则得出函数的导函数,求出常数f'(1)的值,从而确定出函数的解析式是解本题的关键,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
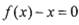 有实数根;
有实数根;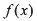 的导数
的导数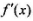 (满足
(满足 ”
” 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;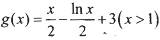 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;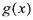 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在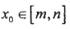 ,使得
,使得 ”,请利用函数
”,请利用函数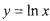 的图象说明这一结论.
的图象说明这一结论.