题目内容
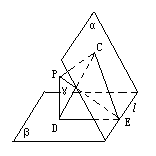
二面角α-l-β内有一点P,若P到平面α,β的距离分别是5,8,且P在平面α,β的内的射影的距离为7,则二面角α-l-β的度数是( )
| A、30° | B、60° | C、120° | D、150° |
分析:设P在平面α,β的内的射影分别为A和B,过A作α与β交线的垂线,垂足为C,连接BC,根据余弦定理求出∠APB=
,根据二面角平面角的定义可知∠ACB即为二面角α-l-β的平面角,最后根据∠ACB与∠APB互补,即可求出所求.
| 1 |
| 2 |
解答:解:设P在平面α,β的内的射影分别为A和B,
过A作α与β交线 的垂线,垂足为C,连接BC,
的垂线,垂足为C,连接BC,
∵PA=5,PB=8,AB=7,
∴cos∠APB=
即∠APB=60°
而∠ACB即为二面角α-l-β的平面角,
∵∠ACB与∠APB互补,
∴∠ACB=120°,
故选C.
过A作α与β交线
 的垂线,垂足为C,连接BC,
的垂线,垂足为C,连接BC,∵PA=5,PB=8,AB=7,
∴cos∠APB=
| 1 |
| 2 |
而∠ACB即为二面角α-l-β的平面角,
∵∠ACB与∠APB互补,
∴∠ACB=120°,
故选C.
点评:本题主要考查了二面角的平面角及求法,求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.

练习册系列答案
相关题目
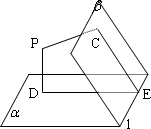
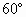 的二面角α-l-β内有一点P,P到α,β的距离分别为PC=2cm,PD=3cm,则垂足的连线CD=________;P到棱l的距离为________.
的二面角α-l-β内有一点P,P到α,β的距离分别为PC=2cm,PD=3cm,则垂足的连线CD=________;P到棱l的距离为________.