题目内容
已知等差数列{an}的首项为1,公差为2,若a1a2-a2a3+a3a4-a4a5+… 对n∈N*恒成立,则实数t的取值范围是 .
对n∈N*恒成立,则实数t的取值范围是 .
【答案】分析:由a1a2-a2a3+a3a4-a4a5+…-a2na2n+1=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)=4(a2+a4+…+a2n),结合等差数列的性质及求和公式可得关于n的不等式,解不等式可求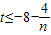 对n∈N*恒成立,转化为求解函数的最值即可
对n∈N*恒成立,转化为求解函数的最值即可
解答:解:a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
=-4(a2+a4+…+a2n)
=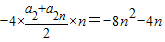 ,
,
所以-8n2+4n≥tn2,
所以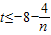 对n∈N*恒成立,
对n∈N*恒成立,
t≤-12,
故答案为(-∞,-12]
点评:本题主要考查了等差数列的性质及求和 公式的应用及恒成立与最值求解的相互转化关系的应用.
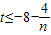 对n∈N*恒成立,转化为求解函数的最值即可
对n∈N*恒成立,转化为求解函数的最值即可解答:解:a1a2-a2a3+a3a4-a4a5+…-a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1-a2n+1)
=-4(a2+a4+…+a2n)
=
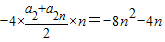 ,
,所以-8n2+4n≥tn2,
所以
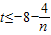 对n∈N*恒成立,
对n∈N*恒成立,t≤-12,
故答案为(-∞,-12]
点评:本题主要考查了等差数列的性质及求和 公式的应用及恒成立与最值求解的相互转化关系的应用.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.