题目内容
已知O为平面直角坐标系的原点,过点M(-2,0)的直线l与圆x2+y2=1交于P、Q两点,且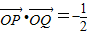 .
.(Ⅰ)求∠PDQ的大小;
(Ⅱ)求直线l的方程.
【答案】分析:(Ⅰ)由点P、Q在圆上可知| |=|
|=| |=1,由
|=1,由 利用向量数量积运算可得cos∠POQ,由此可得答案;
利用向量数量积运算可得cos∠POQ,由此可得答案;
(Ⅱ)易知直线存在斜率,设直线l:y=k(x+2).由(Ⅰ)知点O到直线l的距离为 ,根据点到直线的距离公式可得关于k的方程,解出k代入直线方程即可;
,根据点到直线的距离公式可得关于k的方程,解出k代入直线方程即可;
解答:解:(Ⅰ)因为P、Q两点在圆x2+y2=1上,所以 ,
,
因为 ,所以
,所以 .
.
所以∠POQ=120°.
(Ⅱ)依题意,直线l的斜率存在,
因为直线l过点M(-2,0),可设直线l:y=k(x+2).
由(Ⅰ)可知O到直线l的距离等于 .
.
所以 ,解得k=±
,解得k=± ,
,
所以直线l的方程为x- y+2=0或x+
y+2=0或x+ y+2=0.
y+2=0.
点评:本题考查平面向量数量积的运算、直线与圆相交的性质,属中档题.
 |=|
|=| |=1,由
|=1,由 利用向量数量积运算可得cos∠POQ,由此可得答案;
利用向量数量积运算可得cos∠POQ,由此可得答案;(Ⅱ)易知直线存在斜率,设直线l:y=k(x+2).由(Ⅰ)知点O到直线l的距离为
 ,根据点到直线的距离公式可得关于k的方程,解出k代入直线方程即可;
,根据点到直线的距离公式可得关于k的方程,解出k代入直线方程即可;解答:解:(Ⅰ)因为P、Q两点在圆x2+y2=1上,所以
 ,
,因为
 ,所以
,所以 .
.所以∠POQ=120°.
(Ⅱ)依题意,直线l的斜率存在,
因为直线l过点M(-2,0),可设直线l:y=k(x+2).
由(Ⅰ)可知O到直线l的距离等于
 .
.所以
 ,解得k=±
,解得k=± ,
,所以直线l的方程为x-
 y+2=0或x+
y+2=0或x+ y+2=0.
y+2=0.点评:本题考查平面向量数量积的运算、直线与圆相交的性质,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.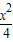 +
+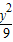 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.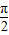 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 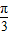 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.