题目内容
已知关于x 的方程x2-|x|+a-1=0有四个不等根,则实数a的取值范围是 .
【答案】分析:已知关于x 的方程x2-|x|+a-1=0有四个不等根,可以分两种情况讨论:①x>0,方程有两正根;②x<0,方程有两负根,分别求出a的范围,再求交集;
解答:解:∵方程x2-|x|+a-1=0有四个不等根,
①若x>0,方程有两正根设为x1,x2,则有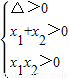 ,△=1-4(a-1)>0,
,△=1-4(a-1)>0,
解得1<a<
②若x<0,方程有两负根设为x1,x2,则有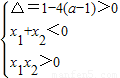 ,
,
解得1<a< ,
,
∴实数a的取值范围是1<a< ,
,
故答案为:(1, ).
).
点评:此题主要考查根的存在及其个数的判断,用到了分类讨论的思想,此题是一道中档题.
解答:解:∵方程x2-|x|+a-1=0有四个不等根,
①若x>0,方程有两正根设为x1,x2,则有
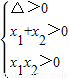 ,△=1-4(a-1)>0,
,△=1-4(a-1)>0,解得1<a<

②若x<0,方程有两负根设为x1,x2,则有
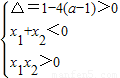 ,
,解得1<a<
 ,
,∴实数a的取值范围是1<a<
 ,
,故答案为:(1,
 ).
).点评:此题主要考查根的存在及其个数的判断,用到了分类讨论的思想,此题是一道中档题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目