题目内容
在△ABC中,角A为锐角,且 +cos2A.
+cos2A.
(1)求f(A)的最大值;
(2)若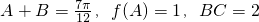 ,求△ABC的三个内角和AC边的长.
,求△ABC的三个内角和AC边的长.
解:(I) 由已知得f(A)=
 ∴
∴ 取值最大值,其最大值为
取值最大值,其最大值为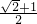
(II)由 f(A)=1得sin(2A+ )=
)=

在△ABC中,由正弦定理得:
分析:(1)先利用诱导公式化简f(A),根据A为锐角,确定f(A)的最大值.
(2)利用f(A)=1求出A、B、C三个角,再用正弦定理求出AC边的长.
点评:本题考查诱导公式的化简求值,二倍角的余弦公式等知识,是中档题.

 ∴
∴ 取值最大值,其最大值为
取值最大值,其最大值为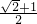
(II)由 f(A)=1得sin(2A+
 )=
)=

在△ABC中,由正弦定理得:

分析:(1)先利用诱导公式化简f(A),根据A为锐角,确定f(A)的最大值.
(2)利用f(A)=1求出A、B、C三个角,再用正弦定理求出AC边的长.
点评:本题考查诱导公式的化简求值,二倍角的余弦公式等知识,是中档题.

练习册系列答案
相关题目
 =(sinx,1+cos2x),
=(sinx,1+cos2x), =(sinx-cosx,cos2x+
=(sinx-cosx,cos2x+ ),定义函数f(x)=
),定义函数f(x)= •(
•( -
- )
) ,求边AC的长.
,求边AC的长. =(sinx,1+cos2x),
=(sinx,1+cos2x), =(sinx-cosx,cos2x+
=(sinx-cosx,cos2x+ ),定义函数f(x)=
),定义函数f(x)= •(
•( -
- )
) ,求边AC的长.
,求边AC的长.