题目内容
已知双曲线(1)求直线AB的方程;
(2)若Q(1,1),证明不存在以Q为中点的弦.
(1)解:设过点P(1,2)的直线AB的方程为y-2=k(x-1),?
代入双曲线方程并整理得(2-k2)x2+(2k2-4k)x-(k2-4k+6)=0.
设A(x1,y1),B(x2,y2),则有x1+x2=![]() .?
.?
由已知![]() ,
,
∴![]() ,解得k=1.
,解得k=1.
又k=1时,Δ=(2k2-4k)2+4(2-k2)(k2-4k+6)=16>0,从而直线AB的方程为x-y+1=0.
(2)证明:设过Q(1,1)点的直线方程为y-1=k(x-1),?
代入双曲线方程并整理,得(2-k2)x2-2k(1-k)x-(k2-2k+3)=0.
由题知![]() ,解得k=2.
,解得k=2.
而当k=2时,Δ=[-2k(1-k)]2+4(2-k2)(k2-2k+3)=-62<0.
∴这样的直线不存在.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
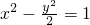 与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为A、B中点.
与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为A、B中点.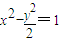 与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为A、B中点.
与点P(1,2),过P点作直线l与双曲线交于A、B两点,若P为A、B中点.