题目内容
函数f（x）=x2+x在[x，x+△x]（其中△x≠0）的平均变化率为（ ）A．2x
B．2x+△
C．2x+1
D．2x+△x+1
【答案】分析：利用函数的解析式求出区间两个端点的函数值；利用平均变化率公式求出该函数在区间[x，x+△x]上的平均变化率．
解答：解：∵函数f（x）=x2+x在[x，x+△x]，
∴f（x+△x）=（x+△x）2+x+△x，f（x）=x2+x，
∴函数f（x）=x2+x在[x，x+△x]（其中△x≠0）的平均变化率为
=
=
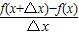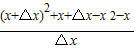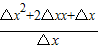=△x+2x+1，
故选D；
点评：本题考查函数在某区间上的平均变化率公式：平均变化率=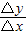
，是一道基础题；
解答：解：∵函数f（x）=x2+x在[x，x+△x]，
∴f（x+△x）=（x+△x）2+x+△x，f（x）=x2+x，
∴函数f（x）=x2+x在[x，x+△x]（其中△x≠0）的平均变化率为
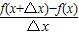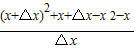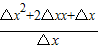===△x+2x+1，故选D；
点评：本题考查函数在某区间上的平均变化率公式：平均变化率=
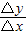，是一道基础题； 
练习册系列答案
53随堂测系列答案
相关题目