题目内容

11．记等比数列{an}的前n项积为Πn，若a4•a5=2，则Π8=16．

分析 根据等比数列的性质，即可得到结论．

解答 解：∵等比数列{an}的前n项积为Πn，
∴Π8=a1•a2a3•a4•a5a6•a7•a8=（a4•a5）4=24=16．
故答案为：16．

点评 本题主要考查等比数列的计算，利用等比数列的性质是解决本题的关键．

练习册系列答案
相关题目
1．已知复数z=3+i（i为虚数单位），则z的共轭复数$\overline z$在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
2．已知定义在R上的函数f（x）的导函数为f′（x），满足f′（x）＜f（x），f（2）=-2，f（1+x）=-f（1-x），则不等式f（x）＜2ex的解集为（　　）
A．（-2，+∞）B．（0，+∞）C．（1，+∞）D．（4，+∞）
19．下列四个函数中，既是奇函数又是定义域上的单调递增的是（　　）
A．y=2-xB．y=tanxC．y=x3D．y=log3x
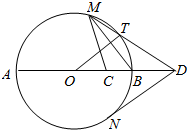6．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连结MC，MB，OT．
（Ⅰ）求证：DT•DM=DO•DC；
（Ⅱ）若∠DOT=30°，求∠BMC．
16．已知函数f（x）=2sinxcosx+cos2x．
（Ⅰ）求f （$\frac{π}{4}$）的值；
（Ⅱ）设α∈（0，$\frac{3}{4}$π），f（$\frac{α}{2}$）=$\frac{1}{5}$，求cos2α的值．
3．已知命题p对任意x∈R，总有|x-1|+|x+1|＞2；命题q：x＞2是x＞1的充分不必要条件．则下列命题为真命题的是（　　）
A．p∧qB．￢p∧￢qC．￢p∧qD．p∧￢q
20．已知向量$\overrightarrow{a}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{b}$=（-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）．
（1）求向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角（用弧度表示）；
（2）设$\overrightarrow{c}$=（cosθ，sinθ），若（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{c}$，求sinθ和cosθ的值．
18．已知函数$f（x）=-aln\frac{1}{x}-b{x^2}$图象上一点P（2，f（2））处的切线方程为y=-3x+2ln2+2．．
（1）求a，b的值；
（2）若方程f（x）+m=0在$[\frac{1}{e}，e]$内有两个不等实根，求m的取值范围（其中e为自然对数的底，e≈2.7）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网