题目内容
【题目】已知函数f（x）= 
x2﹣ax+（3﹣a）lnx，a∈R．
（1）若曲线y=f（x）在点（1，f（1））处的切线与直线2x﹣y+1=0垂直，求a的值；
（2）设f（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求证：f（x1）+f（x2）＞﹣5．
【答案】
（1）解：∵f′（x）=x﹣a+ 
= 
，
∴k=f′（1）=4﹣2a，
∵曲线y=f（x）在点（1，f（1））处的切线与直线2x﹣y+1=0垂直，
∴k=﹣ 
，
∴4﹣2a=﹣ ，
解得a= 
（2）解：由题意，x1，x2为f′（x）=0的两根，
∴ 
，
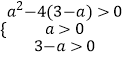∴2＜a＜3，
又∵x1+x2=a，x1x2=3﹣a，
∴f（x1）+f（x2）= （x12+x22）﹣a（x1+x2）+（3﹣a）lnx1x2，
=f（x）=﹣ a2+a﹣3+（3﹣a）ln（3﹣a），
设h（a）=﹣ a2+a﹣3+（3﹣a）ln（3﹣a），a∈（2，3），
则h′（a）=﹣a﹣ln（3﹣a），
∴h″（a）=﹣1+ 
= 
＞0，
故h′（a）在（2，3）递增，又h′（2）=﹣2＜0，
当a→3时，h′（a）→+∞，
∴a0∈（2，3），
当a∈（2，a0）时，h（a）递减，当a∈（a0，3）时，h（a）递增，
∴h（a）min=h（a0）=﹣ a02+a0﹣3+（3﹣a0）ln（3﹣a0）＞﹣ a02+a0﹣3+（3﹣a0）（﹣a0）= a02﹣2a0﹣3= （a0﹣2）2﹣5＞﹣5．
∴a∈（2，3），h（a）＞﹣5，
综上，f（x1）+f（x2）＞﹣5
【解析】（1）根据导数的几何意义即可求出a的值，（2）根据x1 ， x2为f′（x）=0的两根，求出a的范围，再根据韦达定理得到f（x1）+f（x2）=﹣ a2+a﹣3+（3﹣a）ln（3﹣a），构造函数h（a）=﹣ a2+a﹣3+（3﹣a）ln（3﹣a），a∈（2，3），求出函数的最小值大于5即可．
