��Ŀ����
���ں���y=f��x�������������⣺
����a��[-2��2]������f(x)=
�Ķ�����ΪR��
����f(x)=log
(x2-3x+2)����f��x���ĵ���������Ϊ(-�ޣ�
)��
����f(x)=
����ֵ���ǣ�-�ޣ�0���ȣ�0��+�ޣ���
�ܶ�����R�ϵĺ���f��x�������������x��R����f��-x��=-f��x����f��1+x��=f��1-x������4��y=f��x����һ�����ڣ�
����֪a��0��b��0����
+
+2
����Сֵ��4��
����������ı����
����a��[-2��2]������f(x)=
| x2+ax+1 |
����f(x)=log
| 1 |
| 2 |
| 3 |
| 2 |
����f(x)=
| 1 |
| x2-x-2 |
�ܶ�����R�ϵĺ���f��x�������������x��R����f��-x��=-f��x����f��1+x��=f��1-x������4��y=f��x����һ�����ڣ�
����֪a��0��b��0����
| 1 |
| a |
| 1 |
| b |
| ab |
����������ı����
�٢ܢ�
�٢ܢ�
����������f(x)=
�Ķ�����Ϊ{x|x2+ax+1��0}����t=x2+ax+1����a��[-2��2]ʱ����=a2-4��0���ʺ���f(x)=
�Ķ�����ΪR����f(x)=log
(x2-3x+2)�Ķ�������{x|x2-3x+2��0}��
��{x|x��1����x��2}���Գ�����x=
����f��x���ĵ����������ǣ�-�ޣ�1��������y=f(x)=
����yx2-yx-2y-1=0���ɴ˵õ�f(x)=
��ֵ����{y|y��0����y��-
}���ܶ�����R�ϵĺ���f��x����
���������x��R����f��-x��=-f��x����f��1+x��=f��1-x������f��x+4��=f��1-x-3��=f��-x-2��=-f��x+2��=-f��1-x-1��=-f��-x��=f��x������4��y=f��x����һ�����ڣ�����a��0��b��0��֪
+
+2
��2
+2
��2
=4��
| x2+ax+1 |
| x2+ax+1 |
| 1 |
| 2 |
��{x|x��1����x��2}���Գ�����x=
| 3 |
| 2 |
| 1 |
| x2-x-2 |
| 1 |
| x2-x-2 |
| 1 |
| 3 |
���������x��R����f��-x��=-f��x����f��1+x��=f��1-x������f��x+4��=f��1-x-3��=f��-x-2��=-f��x+2��=-f��1-x-1��=-f��-x��=f��x������4��y=f��x����һ�����ڣ�����a��0��b��0��֪
| 1 |
| a |
| 1 |
| b |
| ab |
|
| ab |
2
|
����⣺��f(x)=
�Ķ�����Ϊ{x|x2+ax+1��0}��
��t=x2+ax+1����a��[-2��2]ʱ����=a2-4��0��
��x2+ax+1��0�Ľ⼯��R���ʺ���f(x)=
�Ķ�����ΪR���ʢ���ȷ��
��f(x)=log
(x2-3x+2)�Ķ�������{x|x2-3x+2��0}��
��{x|x��1����x��2}���Գ�����x=
��
��f��x���ĵ����������ǣ�-�ޣ�1�����ʢڲ���ȷ��
����y=f(x)=
����yx2-yx-2y-1=0��
��y��0ʱ����=y2+8y2+4y��0��
���y��0����y��-
��
��y=0ʱ��f(x)=
=0����������
��f(x)=
��ֵ����{y|y��0����y��-
}���ʢ۲�������
�ܶ�����R�ϵĺ���f��x����
���������x��R����f��-x��=-f��x����f��1+x��=f��1-x����
��f��x+4��=f��1-x-3��=f��-x-2��=-f��x+2��=-f��1-x-1��=-f��-x��=f��x����
��4��y=f��x����һ�����ڣ��ʢ���ȷ��
�ݡ�a��0��b��0����
+
+2
��2
+2
��2
=4��
��
+
+2
����Сֵ��4���ʢ���ȷ��
�ʴ�Ϊ���٢ܢݣ�
| x2+ax+1 |
��t=x2+ax+1����a��[-2��2]ʱ����=a2-4��0��
��x2+ax+1��0�Ľ⼯��R���ʺ���f(x)=
| x2+ax+1 |
��f(x)=log
| 1 |
| 2 |
��{x|x��1����x��2}���Գ�����x=
| 3 |
| 2 |
��f��x���ĵ����������ǣ�-�ޣ�1�����ʢڲ���ȷ��
����y=f(x)=
| 1 |
| x2-x-2 |
��y��0ʱ����=y2+8y2+4y��0��
���y��0����y��-
| 1 |
| 3 |
��y=0ʱ��f(x)=
| 1 |
| x2-x-2 |
��f(x)=
| 1 |
| x2-x-2 |
| 1 |
| 3 |
�ܶ�����R�ϵĺ���f��x����
���������x��R����f��-x��=-f��x����f��1+x��=f��1-x����
��f��x+4��=f��1-x-3��=f��-x-2��=-f��x+2��=-f��1-x-1��=-f��-x��=f��x����
��4��y=f��x����һ�����ڣ��ʢ���ȷ��
�ݡ�a��0��b��0����
| 1 |
| a |
| 1 |
| b |
| ab |
|
| ab |
2
|
��
| 1 |
| a |
| 1 |
| b |
| ab |
�ʴ�Ϊ���٢ܢݣ�
���������⿼���������ٵ��жϺ�Ӧ�ã��ǻ����⣮����ʱҪ�������⣬ע�⺯���Ķ��������ԡ�ֵ��������Եĺ������ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
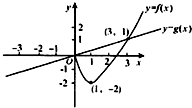 �������ʵ��a��b����max{a��b}=
�������ʵ��a��b����max{a��b}=
|
| A��y=F��x��Ϊ�溯�� |
| B��y=F��x���м���ֵF��1�����м�СֵF��-1�� |
| C��y=F��x������СֵΪ-2�����ֵΪ2 |
| D��y=F��x���ڣ�-3��0���ϲ��ǵ������� |
 �������ʵ��a��b����
�������ʵ��a��b���� ���������ʵ��a��b����max{a��b}=
���������ʵ��a��b����max{a��b}= ���������ʵ��a��b����max
���������ʵ��a��b����max