题目内容
已知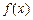 对一切实数
对一切实数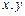 都有
都有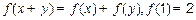 ,当
,当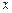 >0时,
>0时,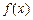 <0
<0
(1)证明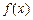 为奇函数;
为奇函数;
(2)证明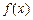 为R上的减函数;
为R上的减函数;
(3)解不等式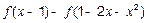 <4.
<4.
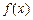 对一切实数
对一切实数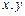 都有
都有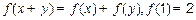 ,当
,当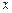 >0时,
>0时,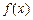 <0
<0(1)证明
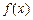 为奇函数;
为奇函数;(2)证明
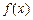 为R上的减函数;
为R上的减函数;(3)解不等式
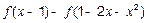 <4.
<4.略
(1)证明:依题意取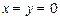 有
有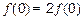
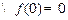 ……………………………………………………………………………1分
……………………………………………………………………………1分
又取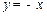 可得
可得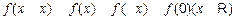
即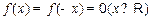
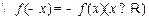 ……………………………………………………………3分
……………………………………………………………3分
由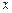 的任意性可知
的任意性可知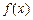 为奇函数……………………………………………………4分
为奇函数……………………………………………………4分
(2)证明:设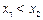 ,则
,则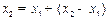 ,其中
,其中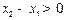 ………………………5分
………………………5分
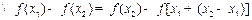
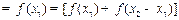
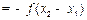 ………………………………………………………………………7分
………………………………………………………………………7分
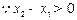
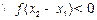
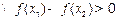 即
即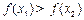
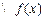 在
在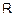 上减函数………………………………………………………………8分
上减函数………………………………………………………………8分
(3)解:依题意有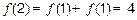 ………………………………………………9分
………………………………………………9分
 不等式可化为
不等式可化为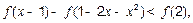
即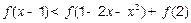
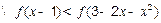 …………………………………………………………10分
…………………………………………………………10分
因为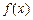 是
是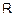 上的减函数
上的减函数
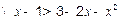 解得
解得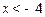 或
或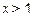 ……………………………………………11分
……………………………………………11分
所以不等式的解集为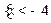 或
或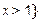 ………………………………………………12分
………………………………………………12分
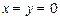 有
有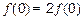
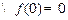 ……………………………………………………………………………1分
……………………………………………………………………………1分又取
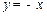 可得
可得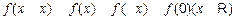
即
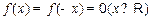
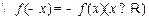 ……………………………………………………………3分
……………………………………………………………3分由
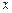 的任意性可知
的任意性可知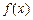 为奇函数……………………………………………………4分
为奇函数……………………………………………………4分(2)证明:设
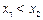 ,则
,则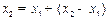 ,其中
,其中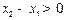 ………………………5分
………………………5分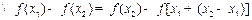
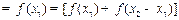
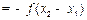 ………………………………………………………………………7分
………………………………………………………………………7分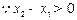
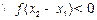
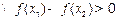 即
即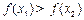
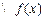 在
在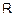 上减函数………………………………………………………………8分
上减函数………………………………………………………………8分(3)解:依题意有
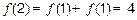 ………………………………………………9分
………………………………………………9分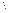 不等式可化为
不等式可化为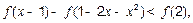
即
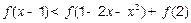
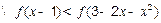 …………………………………………………………10分
…………………………………………………………10分因为
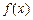 是
是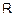 上的减函数
上的减函数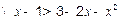 解得
解得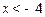 或
或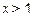 ……………………………………………11分
……………………………………………11分所以不等式的解集为
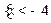 或
或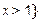 ………………………………………………12分
………………………………………………12分
练习册系列答案
相关题目
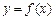 是定义在R上的函数,对于任意的
是定义在R上的函数,对于任意的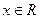 ,
,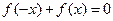 ,且当
,且当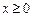 时,
时,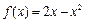 .
.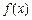 的单调区间及在每个区间上的增减性;
的单调区间及在每个区间上的增减性;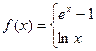
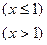 ,那么
,那么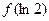 的值是( )
的值是( )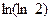
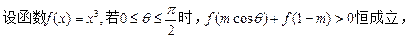
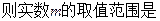
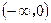

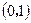
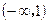
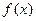 在定义域R内可导,若
在定义域R内可导,若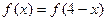 ,且
,且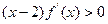 ,记
,记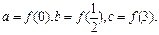 则
则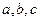 的大小关系是( )
的大小关系是( )
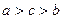
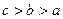
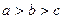
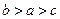
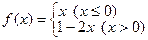 ,则
,则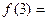 .
.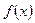 在区间
在区间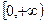 上单调递增,则满足
上单调递增,则满足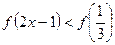 的
的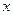 的取值范围是
的取值范围是

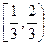
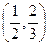
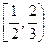
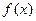 满足:对任意实数a,b都有
满足:对任意实数a,b都有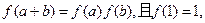
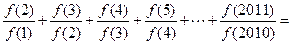 ;
;