题目内容
设等差数列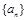 的前n项和为
的前n项和为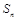 ,且
,且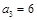 ,
,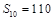 .
.
(Ⅰ)求数列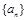 的通项公式;
的通项公式;
(Ⅱ)设数列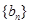 前n项和为
前n项和为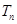 ,且
,且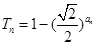 ,令
,令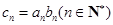 .求数列
.求数列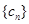 的前n项和
的前n项和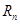 .
.
【答案】
(I)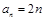 (II)
(II)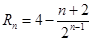 .
.
【解析】
试题分析:此类问题的一般处理方法是,首先依题意,建立“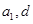 ”的方程组,确定数列
”的方程组,确定数列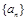 的通项公式,进一步利用
的通项公式,进一步利用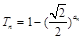 ,应用
,应用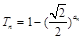 与
与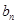 的关系,确定
的关系,确定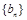 的通项公式.根据数列的特征,利用“错位相减法”求和,属于常考题,易错点是忽视对
的通项公式.根据数列的特征,利用“错位相减法”求和,属于常考题,易错点是忽视对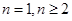 两类情况的讨论.
两类情况的讨论.
试题解析:(Ⅰ)设等差数列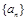 的公差为
的公差为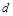 ,
,
∵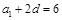 ,
,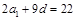 ,
2分
,
2分
∴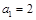 ,
,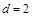 ,
4分
,
4分
所以数列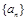 的通项公式
的通项公式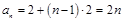 ;
6分
;
6分
(Ⅱ)因为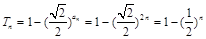 ,
7分
,
7分
当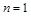 时,
时,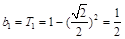 ,
,
当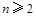 时,
时,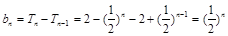 , 10分
, 10分
且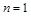 时不满足
时不满足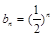 , 11分
, 11分
且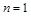 时满足
时满足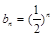 ,
8分
,
8分
所以数列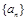 的通项公式为
的通项公式为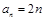 ;
;
所以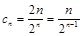 ,
9分
,
9分
所以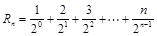 ,
,
即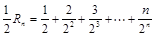 ,
10分
,
10分
两式相减得: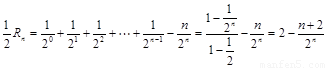 ,
11分
,
11分
所以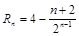 .
12分
.
12分
考点:等差数列的通项公式,数列的前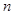 项和与第
项和与第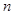 项之间的关系,“错位相减法”.
项之间的关系,“错位相减法”.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
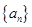 的前n项和为
的前n项和为 ,若
,若 ,
, ,则当
,则当 的前n项和为
的前n项和为 ,且
,且 (c是常数,
(c是常数,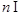 N*),
N*), .
. .
.