Question

（本小题满分12分）

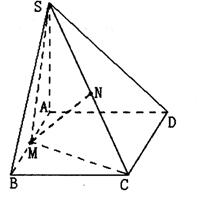
        如图，在四棱锥S—ABCD中，底面ABCD为矩形，SA⊥平面ABCD，二面角S—

CD—A的平面角为，M为AB中点，N为SC中点.

   （1）证明：MN//平面SAD；

   （2）证明：平面SMC⊥平面SCD；

   （3）若，求实数的值，使得直线SM与平面SCD所成角为

Answer 1

略

解析:

证明：取SD中点E，连接AE，NE，

则[来源:学科网ZXXK]

四边形AMNE为平行四边形，

        …………1分

又平面SAD  …………3分

   （2）平面ABCD，

，

底面ABCD为矩形，

又

平面SAD，

    即为二面角S—CD—A的平面角，

即                  …………5分

为等腰直角三角形，

平面SAD，

又平面SCD

平面SCD，[来源:学科网]

平面SMC，

平面SMC平面SCD            …………8分

   （3），设AD=SA=a，则CD

由（2）可得MN平面SCD，

即为SM在平面SCD内的射影

即为直线SM与平面SCD所成角，

即                …………9分

而MN=AE=

中，而[来源:学科网]

中，由得

解得

当时，直线SM与平面SCD所成角为    …………12分