题目内容
△ABC中,角A、B、C的对边分别为a、b、c,且lga﹣lgb=lgcosB﹣lgcosA≠0.
(1)判断△ABC的形状;
(2)设向量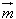 =(2a,b),
=(2a,b), =(a,﹣3b),且
=(a,﹣3b),且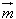 ⊥
⊥ ,(
,(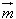 +
+ )(﹣
)(﹣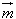 +
+ )=14,求a,b,c.
)=14,求a,b,c.
(1)判断△ABC的形状;
(2)设向量
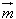 =(2a,b),
=(2a,b), =(a,﹣3b),且
=(a,﹣3b),且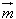 ⊥
⊥ ,(
,(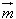 +
+ )(﹣
)(﹣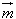 +
+ )=14,求a,b,c.
)=14,求a,b,c.解:(1)由题lga+lgcosA=lgb+lgcosB,
故acosA=bcosB,
由正弦定理sinAcosA=sinBcosB,即sin2A=sin2B.
又cosA>0,cosB>0,
故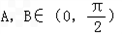 ,2A,2B∈(0,π)
,2A,2B∈(0,π)
因a≠b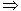 A≠B,故2A=π﹣2B.即
A≠B,故2A=π﹣2B.即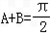 ,
,
故△ABC为直角三角形
(2)由于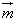 ⊥
⊥ ,所以2a2﹣3b2=0①
,所以2a2﹣3b2=0①
且(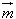 +
+ )(﹣
)(﹣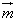 +
+ )=
)= 2﹣
2﹣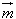 2=14,
2=14,
即8b2﹣3a2=14 ②
由①②解得a2=6,b2=4,
故在直角△ABC中,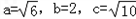
故acosA=bcosB,
由正弦定理sinAcosA=sinBcosB,即sin2A=sin2B.
又cosA>0,cosB>0,
故
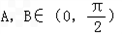 ,2A,2B∈(0,π)
,2A,2B∈(0,π)因a≠b
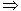 A≠B,故2A=π﹣2B.即
A≠B,故2A=π﹣2B.即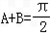 ,
,故△ABC为直角三角形
(2)由于
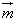 ⊥
⊥ ,所以2a2﹣3b2=0①
,所以2a2﹣3b2=0①且(
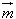 +
+ )(﹣
)(﹣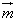 +
+ )=
)= 2﹣
2﹣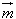 2=14,
2=14,即8b2﹣3a2=14 ②
由①②解得a2=6,b2=4,
故在直角△ABC中,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目