题目内容
已知f（
+1）=x-1，则f（x）=________（x∈________）．
x2-2x， [1，+∞）
分析：采用换元法求该函数的解析式．
解答：令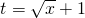
，则t≥1，x=（t-1）2，
所以f（t）=（t-1）2-1=t2-2t，
所以f（x）=x2-2x，x∈[1，+∞）．
故答案为x2-2x，x∈[1，+∞）．
点评：本题考察函数解析式的求解，换元法是经常考察的，换元法中要注意换元后注意新元的范围．
分析：采用换元法求该函数的解析式．
解答：令
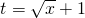，则t≥1，x=（t-1）2，所以f（t）=（t-1）2-1=t2-2t，
所以f（x）=x2-2x，x∈[1，+∞）．
故答案为x2-2x，x∈[1，+∞）．
点评：本题考察函数解析式的求解，换元法是经常考察的，换元法中要注意换元后注意新元的范围．
练习册系列答案
阅读快车系列答案
相关题目
已知f（
）=
，则f（x）的解析式为（ ）
| 1-x |
| 1+x |
| 1-x2 |
| 1+x2 |
A、f（x）=
| ||
B、f（x）=-
| ||
C、f（x）=
| ||
D、f（x）=-
|
；
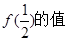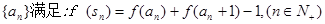其中sn是数列
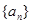的前n项和，求