题目内容
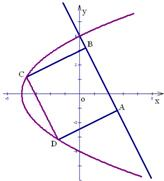 矩形ABCD的顶点A、B在直线l:2x+y-4=0上运动,点C,D曲线E:y2=4(x+4)(-4≤x≤4)上运动,求矩形ABCD面积的最大值.
矩形ABCD的顶点A、B在直线l:2x+y-4=0上运动,点C,D曲线E:y2=4(x+4)(-4≤x≤4)上运动,求矩形ABCD面积的最大值.分析:由题意可知曲线是抛物线的一段,联立直线l:2x+y-4=0与抛物线y2=4(x+4)可求直线与抛物线的交点,结合-4≤x≤4,点(5,-6)不是直线l与曲线E的交点.则可知C、D只能在直线的左侧.,设直线CD的方程为:2x+y-b=0,由CD在直线l的左侧知:过点(4,-4
)可得b≤8-4
,
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
设C、D两点的横坐标为x1,x2,则由方程的根与系数关系及弦长公式可求CD,结合|BC|=
,则可得矩形ABCD的面积S=|CD|•|BC|=
•(4-b),(-
<b<8-4
)
(法一)利用导数知识判断函数y=S2=(2b+17)(4-b)2=2b3+b2-104b+272的单调性,进而可求函数的最大值
(法二)S=|CD|•|BC|=
•(4-b),(-
<b<8-4
),利用基本不等式可求函数的最大值
| 2 |
| 2 |
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
| 17 |
| 2 |
| |4-b| | ||
|
| 2b+17 |
| 17 |
| 2 |
| 2 |
(法一)利用导数知识判断函数y=S2=(2b+17)(4-b)2=2b3+b2-104b+272的单调性,进而可求函数的最大值
(法二)S=|CD|•|BC|=
| 2b+17 |
| 17 |
| 2 |
| 2 |
解答:解:(法一)由题意可知曲线是抛物线的一段,联立直线l:2x+y-4=0与抛物线y2=4(x+4)
可得
,解得
或
因为-4≤x≤4,所以(5,-6)不是直线l与曲线E的交点.故C、D只能在直线的左侧.
设直线CD的方程为:2x+y-b=0,其中b为截距,由CD在直线l的左侧知:过点(4,-4
)时,b取最大值,得b≤8-4
,
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,
由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
-----------(5分).
设C、D两点的横坐标为x1,x2,则x1+x2=b+1,x1x2=
,
∴CD=
=
,又|BC|=
-----------(8分),
从而矩形ABCD的面积S=|CD|•|BC|=
•(4-b),(-
<b<8-4
)--(10分).
令y=S2=(2b+17)(4-b)2=2b3+b2-104b+272,
y′=6b2+2b-104=(b-4)(6b+26),
当-
<b<-
时,y′>0,函数y=2b3+b2-104b+272,在(-
,-
)上单调递增
-
<b<8-4
时,y′<0,函数y=2b3+b2-104b+272,在[-
,8-4
)上单调递减
所以,b=-
时,S取极大值,也是最大值,
矩形ABCD的面积的最大值为
-----------(15分).
(法二)由题意可知曲线是抛物线的一段,联立直线l:2x+y-4=0与抛物线y2=4(x+4)
可得
,解得
或
因为-4≤x≤4,所以(5,-6)不是直线l与曲线E的交点.故C、D只能在直线的左侧.
设直线CD的方程为:2x+y-b=0,其中b为截距,由CD在直线l的左侧知:过点(4,-4
)时,b取最大值,得b≤8-4
,
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,
由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
-----------(5分).
设C、D两点的横坐标为x1,x2,则x1+x2=b+1,x1x2=
,
∴CD=
=
,又|BC|=
-----------(8分),
从而矩形ABCD的面积S=|CD|•|BC|=
•(4-b),(-
<b<8-4
)--(10分).
∵(2b+17)+(4-b)+(4-b)=25
∴S=
•(4-b)=
•
•
≤
=
=
当且仅当2b+17=4-b时,即b=-
时取得最大值.
可得
|
|
|
因为-4≤x≤4,所以(5,-6)不是直线l与曲线E的交点.故C、D只能在直线的左侧.
设直线CD的方程为:2x+y-b=0,其中b为截距,由CD在直线l的左侧知:过点(4,-4
| 2 |
| 2 |
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,
由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
| 17 |
| 2 |
设C、D两点的横坐标为x1,x2,则x1+x2=b+1,x1x2=
| b2-16 |
| 4 |
∴CD=
| 5[(x1+x2)2-4x1x2] |
| 5(2b+17) |
| |4-b| | ||
|
从而矩形ABCD的面积S=|CD|•|BC|=
| 2b+17 |
| 17 |
| 2 |
| 2 |
令y=S2=(2b+17)(4-b)2=2b3+b2-104b+272,
y′=6b2+2b-104=(b-4)(6b+26),
当-
| 17 |
| 2 |
| 13 |
| 3 |
| 17 |
| 2 |
| 13 |
| 3 |
-
| 13 |
| 3 |
| 2 |
| 13 |
| 3 |
| 2 |
所以,b=-
| 13 |
| 3 |
矩形ABCD的面积的最大值为
125
| ||
| 9 |
(法二)由题意可知曲线是抛物线的一段,联立直线l:2x+y-4=0与抛物线y2=4(x+4)
可得
|
|
|
因为-4≤x≤4,所以(5,-6)不是直线l与曲线E的交点.故C、D只能在直线的左侧.
设直线CD的方程为:2x+y-b=0,其中b为截距,由CD在直线l的左侧知:过点(4,-4
| 2 |
| 2 |
由y2=4(x+4)及2x+y-b=0,消去y得4x2-(4b+4)x+b2-16=0,
由△=(4b+4)2-4•4•(b2-16)=16(2b+17)>0,得b>-
| 17 |
| 2 |
设C、D两点的横坐标为x1,x2,则x1+x2=b+1,x1x2=
| b2-16 |
| 4 |
∴CD=
| 5[(x1+x2)2-4x1x2] |
| 5(2b+17) |
| |4-b| | ||
|
从而矩形ABCD的面积S=|CD|•|BC|=
| 2b+17 |
| 17 |
| 2 |
| 2 |
∵(2b+17)+(4-b)+(4-b)=25
∴S=
| 2b+17 |
| 2b+17 |
| 4-b |
| 4-b |
(
|
(
|
125
| ||
| 9 |
当且仅当2b+17=4-b时,即b=-
| 13 |
| 3 |
点评:本题主要考查了直线与抛物线的相交关系的应用,方程的根与系数关系的应用,及利用导数知识判断函数的 单调性,求解函数的最值及利用基本不等式求解函数的最值,属于函数知识的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
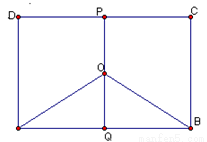
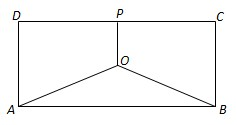 某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm.
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm. (I)按下列要求写出函数关系式:
(I)按下列要求写出函数关系式: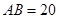 km,
km, 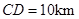 ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。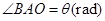 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;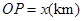 ,将
,将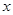 的函数关系式。
的函数关系式。