题目内容
已知函数f(x)=lnx-ax(a∈R).(1)当a=2时,求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上最小值.
【答案】分析:(1)先确定函数f(x)的定义域,然后对函数f(x)求导,根据导函数大于0时原函数单调递增,导函数小于0时原函数单调递减求出单调区间;
(2)分类讨论,确定函数的单调性,从而可确定函数的最值.
解答:解:(1)当a=2时,f(x)=lnx-ax,函数f(x)的定义域为(0,+∞),
求导函数可得f'(x)=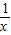 -2
-2
①由f'(x)>0,x>0,得0<x<
②由f'(x)<0,x>0,得x>
故函数f(x)的单调递增区间为(0, ),单调减区间是(
),单调减区间是( ,+∞).…(8分)
,+∞).…(8分)
(2)①当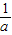 ≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
∴f(x)的最小值是f(2)=ln2-2a.…(10分)
②当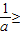 2,即a≤
2,即a≤ 时,函数f(x)在区间[1,2]上是增函数,
时,函数f(x)在区间[1,2]上是增函数,
∴f(x)的最小值是f(1)=-a.…(12分)
③当1<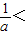 2,即
2,即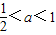 时,函数f(x)在[1,
时,函数f(x)在[1,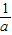 ]上是增函数,在[
]上是增函数,在[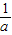 ,2]上是减函数.
,2]上是减函数.
又f(2)-f(1)=ln2-a,
∴当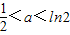 时,最小值是f(1)=-a;
时,最小值是f(1)=-a;
当ln2≤a<1时,最小值为f(2)=ln2-2a.…(15分)
综上可知,当0<a<ln2时,函数f(x)的最小值是-a;当a≥ln2时,函数f(x)的最小值是ln2-2a.…(16分)
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查函数的最值,正确求导,确定分类标准是关键.
(2)分类讨论,确定函数的单调性,从而可确定函数的最值.
解答:解:(1)当a=2时,f(x)=lnx-ax,函数f(x)的定义域为(0,+∞),
求导函数可得f'(x)=
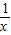 -2
-2①由f'(x)>0,x>0,得0<x<

②由f'(x)<0,x>0,得x>

故函数f(x)的单调递增区间为(0,
 ),单调减区间是(
),单调减区间是( ,+∞).…(8分)
,+∞).…(8分)(2)①当
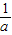 ≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,
≤1,即a≥1时,函数f(x)在区间[1,2]上是减函数,∴f(x)的最小值是f(2)=ln2-2a.…(10分)
②当
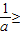 2,即a≤
2,即a≤ 时,函数f(x)在区间[1,2]上是增函数,
时,函数f(x)在区间[1,2]上是增函数,∴f(x)的最小值是f(1)=-a.…(12分)
③当1<
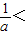 2,即
2,即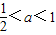 时,函数f(x)在[1,
时,函数f(x)在[1,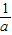 ]上是增函数,在[
]上是增函数,在[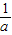 ,2]上是减函数.
,2]上是减函数.又f(2)-f(1)=ln2-a,
∴当
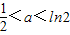 时,最小值是f(1)=-a;
时,最小值是f(1)=-a;当ln2≤a<1时,最小值为f(2)=ln2-2a.…(15分)
综上可知,当0<a<ln2时,函数f(x)的最小值是-a;当a≥ln2时,函数f(x)的最小值是ln2-2a.…(16分)
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查函数的最值,正确求导,确定分类标准是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目