题目内容
已知向量a,b是互相垂直的单位向量,且 ,则对任意的实数
,则对任意的实数
 的最小值为( )
的最小值为( )
| A.5 | B.7 | C.12 | D.13 |
C
解析试题分析:因为由题意可知,|a|="|b|=1," b.a =0,c.a="3," c.b=4,|c|=13,那么可知|c-t1a-t2b|2=c2+ t12a2+ t22b2-2 t1c.a-2 t2c.b+2t1 t2b.a=132+ t12+ t22-6 t1-8 t2= (t1-3)2+(t2-4)2+144 144,故其模长的最小值为12,选C.
144,故其模长的最小值为12,选C.
考点:本试题主要考查了向量的数量积的运算,以及求解斜率的模长的运用。
点评:解决该试题的关键是处理向量的长度问题,往往是将其平方,转化为向量的数量积公式来得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点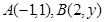 ,向量
,向量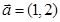 ,若
,若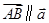 ,则实数
,则实数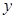 的值为
的值为
| A.5 | B.6 | C.7 | D.8 |
已知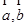 均为单位向量,它们的夹角为60°,那么,
均为单位向量,它们的夹角为60°,那么,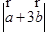 等于( )
等于( )
A. | B.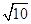 | C.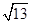 | D.4 |
已知向量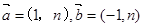 ,若
,若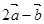 与
与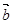 垂直,则
垂直,则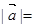 ( )
( )
A.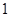 | B.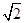 | C.4 | D.2 |
已知 且
且 与
与 垂直,则实数
垂直,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
已知平面向量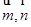 的夹角为
的夹角为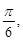 且
且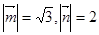 ,在
,在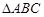 中,
中,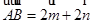 ,
,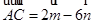 ,
,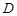 为
为 中点,则
中点,则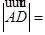 ( )
( )
| A.2 | B.4 | C.6 | D.8 |
已知向量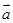 、
、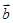 不共线,
不共线, ,如果
,如果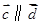 ,那么
,那么
A.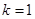 且 且 与 与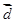 同向 同向 | B.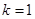 且 且 与 与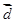 反向 反向 |
C.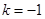 且 且 与 与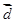 同向 同向 | D.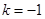 且 且 与 与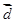 反向 反向 |
已知向量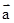 ,
,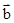 满足
满足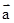 ·
·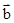 =0,│
=0,│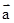 │=1,│
│=1,│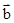 │=2,则│2
│=2,则│2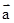 -
-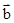 │=( )
│=( )
| A.0 | B.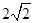 | C. 4 | D.8 |
设向量a.b满足 ( )
( )
A. | B. | C. | D. |