题目内容
(2010•通州区一模)已知数列{an}的前n项和Sn=n2an-n(n-1)(n∈N*),且a1=
.
(I)求a2与a3;
(II)求证:数列{
Sn}是等差数列;
(III)试比较a1+2a2+3a3+…+nan与2n+1-n-2的大小,并说明理由.
| 1 |
| 2 |
(I)求a2与a3;
(II)求证:数列{
| n+1 |
| n |
(III)试比较a1+2a2+3a3+…+nan与2n+1-n-2的大小,并说明理由.
分析:(Ⅰ)利用Sn=n2an-n(n-1)(n∈N*),n分别取2,3代入,结合a1=
,可求a2与a3的值;
(II)由 an=Sn-Sn-1 (n≥2),结合条件可得
Sn -
Sn-1=1,结论得证.
(Ⅲ)由(Ⅱ)知,
Sn=1+(n-1)•1=n,Sn=
,根据Sn=n2an-n(n-1),可得
=n2an-n(n-1),从而有nan=(n+1)-
-1,利用 2n=(1+1)n=1+n+…+Cnn≥1+n,得
≥
,从而有nan=(n+1)-
-1≤2n-
-1,故a1+2a2+3a3+…+nan≤(2-
-1)+(2 2-
-1)+…+(2 n-
-1),利用分组求和即可得结论.
| 1 |
| 2 |
(II)由 an=Sn-Sn-1 (n≥2),结合条件可得
| n+1 |
| n |
| n |
| n-1 |
(Ⅲ)由(Ⅱ)知,
| n+1 |
| n |
| n2 |
| n+1 |
| n2 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 2 |
| 1 |
| 2 n |
解答:解:(Ⅰ)∵Sn=n2an-n(n-1)(n∈N*),
∴S2=4a2-2=a1+a2,S3=9a3-6=a1+a2+a3,
∵a1=
,
∴a2=
,a3=
.
(Ⅱ)证明:由 an=Sn-Sn-1 (n≥2),及 Sn=n2an-n(n-1)得
Sn=n2(Sn-Sn-1)-n(n-1),即 (n2-1 )Sn-n2Sn-1=n(n-1),
∴
Sn -
Sn-1=1,
∵a1=
,∴n=1时,
Sn=1
∴{
Sn}是首项为1,公差为1的等差数列.
(Ⅲ)由(Ⅱ)知,
Sn=1+(n-1)•1=n,
∴Sn=
,
又已知Sn=n2an-n(n-1),
∴
=n2an-n(n-1),
∴nan=
+n-1=(n+1)-
-1.
∵2n=(1+1)n=Cn0+Cn1+…+Cnn≥1+n,
∴
≥
,
∴-
≤-
,
∴nan=(n+1)-
-1≤2n-
-1
∴a1+2a2+3a3+…+nan≤(2-
-1)+(2 2-
-1)+…+(2 n-
-1)
=(2+22+…+2n)-(
+
+…+
)-n
=
-
-n
=2n+1-2+
-1-n
∵当n∈N*时,
<1,即
-1<0,
∴2n+1-2+
-1-n<2n+1-n-2.
即a1+2a2+3a3+…+nan<2n+1-n-2
∴S2=4a2-2=a1+a2,S3=9a3-6=a1+a2+a3,
∵a1=
| 1 |
| 2 |
∴a2=
| 5 |
| 6 |
| 11 |
| 12 |
(Ⅱ)证明:由 an=Sn-Sn-1 (n≥2),及 Sn=n2an-n(n-1)得
Sn=n2(Sn-Sn-1)-n(n-1),即 (n2-1 )Sn-n2Sn-1=n(n-1),
∴
| n+1 |
| n |
| n |
| n-1 |
∵a1=
| 1 |
| 2 |
| n+1 |
| n |
∴{
| n+1 |
| n |
(Ⅲ)由(Ⅱ)知,
| n+1 |
| n |
∴Sn=
| n2 |
| n+1 |
又已知Sn=n2an-n(n-1),
∴
| n2 |
| n+1 |
∴nan=
| n |
| n+1 |
| 1 |
| n+1 |
∵2n=(1+1)n=Cn0+Cn1+…+Cnn≥1+n,
∴
| 1 |
| n+1 |
| 1 |
| 2n |
∴-
| 1 |
| n+1 |
| 1 |
| 2n |
∴nan=(n+1)-
| 1 |
| n+1 |
| 1 |
| 2n |
∴a1+2a2+3a3+…+nan≤(2-
| 1 |
| 2 |
| 1 |
| 2 2 |
| 1 |
| 2 n |
=(2+22+…+2n)-(
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=
| 2(1-2n) |
| 1-2 |
| ||||
1-
|
=2n+1-2+
| 1 |
| 2n |
∵当n∈N*时,
| 1 |
| 2n |
| 1 |
| 2n |
∴2n+1-2+
| 1 |
| 2n |
即a1+2a2+3a3+…+nan<2n+1-n-2
点评:本题以数列递推式为载体,考查数列递推式的运用,考查等差数列的定义,考查放缩法,解题的关键是合理运用数列递推式.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
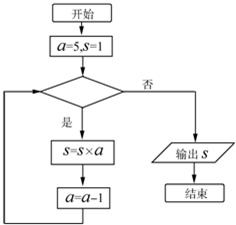 (2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
(2010•通州区一模)执行图所示的程序,输出的结果为20,则判断框中应填入的条件为( )
 (2010•通州区一模)设不等式组
(2010•通州区一模)设不等式组